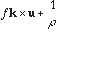
On the influence of the parameterization of lateral boundary layers
on the thermohaline circulation in coarse-resolution ocean models
T
HIERRY HUCK AND ANDREW J. WEAVERSchool of Earth and Ocean Sciences, University of Victoria, P. O. Box 3055, Victoria, BC, V8W 3P6, Canada
A
LAIN COLIN DE VERDIÈRELaboratoire de Physique des Océans, Université de Bretagne Occidentale, B. P. 809, 29285 Brest cedex, France
Submitted to:
Journal of Marine Research
August 1998
Revised:
February 1999
Because of the first order geostrophic balance in the ocean interior, the parameterization of lateral boundary layers has more influence than the parameterization of viscosity on the thermohaline overturning and the deep water properties in coarse-resolution ocean circulation models. Different formulations of momentum dissipation and associated boundary conditions are implemented within a planetary-geostrophic ocean circulation model for a Cartesian coordinate, flat-bottomed,
b-plane, with restoring boundary conditions for the surface density and zero wind stress. Traditional Laplacian friction with a no-slip boundary condition produces an interior circulation in good agreement with geostrophy and the Sverdrup balance, but generates very large vertical (diapycnal) transports at lateral boundaries, especially upwelling in the western boundary current and downwelling in the north-east corner. The meridional and zonal overturning are thus enhanced, but drive to depth surface waters that are not as cold as the ones in the deep convection regions.Rayleigh friction with various frictional closures for the along-shore velocities within a no-normal-flow boundary condition framework efficiently reduces the diapycnal vertical transports along the boundaries, by allowing horizontal recirculation of geostrophic currents impinging into coasts. Hence, these parameterizations induce weaker overturnings, with colder deep water and a sharper thermocline resulting in higher poleward heat transports.
We suggest that the upwelling along the boundaries is a consequence of the coarse-resolution dynamics and not only horizontal diffusion (termed the "Veronis effect", horizontal diffusion produces large diapycnal fluxes once the isopycnals are tilted by coastal upwellings). Alternative parameterizations for the lateral boundary layers reduce this effect without the need for rotating the mixing tensor along isopycnals. This model comparison proves the need to clearly assess the extent of the diapycnal upwelling in the western boundary currents and to develop physically-based parameterizations of lateral boundary layers in order to improve coarse-resolution OGCMs.
A fundamental role of the ocean in the climate system is its ability to store and transport heat poleward. In the North Atlantic, the main contribution to the poleward heat transfer is related to the thermohaline overturning (Bryan, 1962), driven by the formation of deep water in the northern seas. Hence, accurately modeling the thermohaline circulation is a crucial task for climate studies. Most current models are run at coarse resolution, the grid-spacing being an order of magnitude larger than the Rossby radius of deformation. These models must then rely on the parameterization of sub-grid-scale processes, including the effect of the most energetic mesoscale eddies on tracer and momentum (mixing and advection). Although the large scale thermohaline overturning is captured in these coarse-resolution simulations, many aspects of the results need to be improved: the thermocline is often too deep, the deep temperature and salinity fields are often too warm and fresh, respectively and the poleward heat transport in the North Atlantic is typically too weak (Bryan, 1987).
Böning et al. (1995) point out the upwelling in the western boundary current (WBC hereafter) as primarily responsible for this weakness through its role as a shortcut of the thermohaline cell. Veronis (1975) explained that this upwelling of cold water is necessary to balance the spurious cross-isopycnal fluxes due to horizontal diffusion across steeply sloping isopycnals in the WBC. These cold waters that cannot make their way southward, significantly reduce the poleward heat transport, hence the whole efficiency of the thermohaline loop is compromised. Böning et al. suggest that this phenomenon will not be avoided unless the Rossby radius of deformation is resolved. We will show that this upwelling is indeed reduced by implementing various parameterizations for lateral boundary layers.
During the last decade, most improvements in global ocean circulation modeling have focused on the sub-grid scale parameterizations for tracers: Isopycnal mixing (Redi, 1982; Cox, 1987) along with a recent parameterization of mesoscale eddy-induced transport of tracers (Gent and McWilliams, 1990) reduces this upwelling, in agreement with the Veronis theory, although this is sometimes limited by numerical constraints on standard advection schemes or computational cost (Weaver and Eby, 1997). These parameterizations lead to significant improvements concerning the regions of deep-water formation and the water mass characteristics (Danabasoglu et al., 1994; Danabasoglu and McWilliams 1995; Hirst and McDougall 1996). They have been shown to induce colder deep water (Robitaille and Weaver, 1995) due to stronger Antarctic bottom water formation and more pronounced North Atlantic deep water penetration in the Equatorial region, and consequently a less diffuse thermocline. The eddy-induced bolus velocities also directly reduce the upwelling felt by the tracers in the WBC (Lazar et al. 1999).
The momentum balance of these models is rarely questioned despite the equivalence of isopycnal mixing of potential vorticity (or isopycnal thickness) and vertical mixing of momentum (Rhines and Young, 1982; Greatbatch and Lamb, 1990; Gent et al., 1995; Tandon and Garrett, 1996). Momentum dissipation is traditionally parameterized through Laplacian diffusion, copied on molecular viscosity, given its good conservation and numerical properties. In eddy-resolving experiments, the more scale-selective biharmonic operator is used to enhance the eddy kinetic energy (Semtner and Chervin, 1988). But at coarse resolution, few alternatives have emerged to parameterize the Reynolds stresses in the momentum equations for representing barotropic and especially baroclinic instabilities (Gent and McWilliams, 1996), and non-necessarily downgradient momentum fluxes occurring in WBCs. The departure from geostrophy is necessary to produce a thermohaline circulation because to avoid mass fluxes across ocean boundaries with geostrophic velocities, the pressure has to be uniform along the walls (as at zeroth order in quasi-geostrophic models). If the pressure at a given latitude is the same at both western and eastern boundaries, no net meridional geostrophic flow can be forced at any depth, at least in the absence of bottom topography. Although dissipation is essential, the choice of boundary conditions (no-slip, free-slip or no-normal-flow) are not well justified at coarse resolution (Stewart, 1989), and the parameterization of lateral boundary layers is rarely implemented (Seidov, 1996).
Zhang et al. (1992) demonstrated that at coarse-resolution, a purely geostrophic model with linear momentum dissipation for the barotropic flow can reproduce the results of the primitive equations (Bryan-Cox) for the evolution of tracer fields, but both are based on the same no-slip boundary condition. Lateral boundary layers, with their intense boundary currents, eddy kinetic energy, and upwellings (the California current for example) may significantly contribute to the global vertical transports, particularly crucial for the baroclinic thermohaline circulation. Even for the wind-driven circulation, the lateral boundary conditions influence the separation of the Gulf Stream for instance (Chassignet and Gent, 1991; Verron and Blayo, 1996).
Upwelling-downwelling adjacent to model boundaries have long been observed in such numerical ocean calculations but their significance has often been played down following Veronis (commenting upon Holland’s work) who attributed WBC upwelling to unrealistically large lateral diffusivity coefficients. Various authors have also related the downwelling region east of the WBC to the horizontal diffusion through analytical, statistical and numerical methods (Masuda and Uehara, 1992; Gough and Welch, 1994; Lazar et al., 1999), although no clear relation has been proved with the intensity of the western upwelling. In contrast, we emphasize in what follows the dynamical aspect of the same problem that appears when geostrophic flows meet solid boundaries. At the coarse resolution of climate models the viscous boundary layers are not resolved and we show that significant differences in the intensity of upwellings occur from different parameterizations of the boundary layers under the same diffusivities. There is of course a lot of uncertainties about the intensity of upwellings in the real ocean. However Csanady (1989) suggested that upwelling was a necessary consequence of potential energy conversion to the eddies and ultimate dissipation. Using a two-level model forced by heating and cooling, Huang and Yang (1996) have shown analytically how the upwelling in the WBC arise naturally from ageostrophic dynamics to obtain a closed heat budget through advection without invoking eddy diffusivities.
In order to clarify the role of the parameterizations for momentum dissipation and lateral boundary layers in coarse resolution thermohaline circulation models, we perform a precise comparison in the same mainframe model, based on the planetary-geostrophic equations. To simplify the analysis, an idealized box-geometry is chosen for a Cartesian, mid-latitude,
b-plane ocean forced by restoring boundary conditions at the surface and zero wind stress. Indeed, the steady state solutions show large discrepancies in terms of temperature and velocity fields, overturnings and global energy balance. Most of the differences are linked to vertical transports along the lateral boundaries (especially north-south).The outline of the rest of this paper is as follows: in the next section, we introduce the models based on the planetary geostrophic dynamics together with the various parameterizations for momentum dissipation and lateral boundary layers (more details are given in the Appendix). Section 3 discusses their implications for the mean circulation and stratification, focusing on the role of the upwelling along the western boundary on the overall thermohaline circulation efficiency. Section 4 analyzes the models energetics concentrating on the convective and dissipative depletion of potential energy in relation to the lateral boundary conditions. Section 5 discusses the physics of the upwelling while section 6 presents the conclusions.
a. The planetary geostrophic dynamics
The present model comparison is carried out in Cartesian coordinates to simplify the set of equations and gain in tractability and understanding. Although the use of these coordinates is not appropriate at the scale of an oceanic basin circulation, we expect only minor deviations in the behavior of the model results when spherical coordinates are employed in our test basin restricted to a mid-latitude
b-plane. As our primary concern is the sensitivity of the thermohaline circulation to various momentum dissipation and lateral boundary layers parameterizations, the non-linear interaction with the wind-driven circulation is ignored and only thermal variations are considered as a simple and meaningful way of dealing with density.A scale analysis of the primitive equations (PE hereafter) for typical coarse-resolution climatic studies shows that time derivatives and non-linear terms can be neglected in the momentum equations, given that the time scale is much larger than a day or so and the spatial scale is much larger than the internal Rossby radius of deformation (Phillips, 1963; Hasselmann, 1982). We can easily assess this simplification with the use of the Rossby number, which measures the ratio of the nonlinear terms to the Coriolis term: Ro=U/(f
l)=O(10-2) for typical western boundary velocities U of 0.1 m s-1, Coriolis parameter f typical of mid-latitudes and grid size l of 100 km. Since Robinson and Stommel (1959) and Welander (1959), numerous ocean models have used this simplified set of equations known as the planetary geostrophic (PG further) or thermocline equations (see Veronis, 1973 for a review): 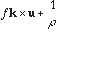
![]()
where x (u) refers to the west-east axis (velocity), y (v) to the south-north axis (velocity) and z (w) to the vertical axis (velocity) oriented upward; r is the density, linearly related to temperature T through a constant thermal expansion coefficient (a=2¥10-4 K-1 and r0=1000 kg m-3); f is the Coriolis parameter equal to f0+by. The surface boundary condition is ![]() , where Q is the surface heat flux [W m-2], distributed over the mixed layer depth assumed uniformly equal to the first level depth, and CP is the specific heat capacity of sea water. Q is parameterized as a restoring boundary condition to the surface climatology following Haney (1971): Q=Q2(T*-T1), where Q2 is a constant related to the restoring time scale, T* the equivalent restoring atmospheric temperature and T1 the temperature of the first ocean level. Since we focus on the momentum equations, the mixing of tracers follows the simplest choice, with spatially uniform horizontal and vertical eddy diffusivities.
, where Q is the surface heat flux [W m-2], distributed over the mixed layer depth assumed uniformly equal to the first level depth, and CP is the specific heat capacity of sea water. Q is parameterized as a restoring boundary condition to the surface climatology following Haney (1971): Q=Q2(T*-T1), where Q2 is a constant related to the restoring time scale, T* the equivalent restoring atmospheric temperature and T1 the temperature of the first ocean level. Since we focus on the momentum equations, the mixing of tracers follows the simplest choice, with spatially uniform horizontal and vertical eddy diffusivities.
The main characteristic of the PG equations is the absence of time derivatives in the momentum equations, which then become diagnostic. Hence, the integration procedure is straightforward, especially when the barotropic mode is zero as a consequence of no wind forcing, no bottom friction and flat bottom: a baroclinic pressure field is computed from the density field via the hydrostatic equation, the horizontal baroclinic velocity field is then determined from the momentum equations, the vertical velocities are then derived from the continuity equation. Only the full prognostic equations for the tracers remain to be integrated in time.
Dissipation is usually added in the horizontal momentum equations to represent the sub-grid scale transfers of energy and to allow the velocity field to match the boundary conditions. The relationship between momentum dissipation, dynamical boundary conditions, tracer diffusion and boundary conditions requires special attention to end up with a well-posed set of momentum and tracer equations (Samelson and Vallis, 1997a).
In order to have a widely used reference and to assess the simplifications we make in our PG models, we compare our results with those obtained with the full PE of the MOM (Modular Ocean Model, Geophysical Fluid Dynamic Laboratory: Pacanowski et al., 1991) for the same flat-bottomed, Cartesian, b-plane, rectangular basin with Laplacian viscosity and no-slip boundary conditions. As in the PG experiments, the wind-stress is zero, the equation of state is a linear function of temperature only and restoring boundary conditions are applied to the surface temperature. We first show the negligible role of the vertical viscosity given the large horizontal viscosity coefficients required to solve for the frictional boundary layers (exp. 1 and 2 in Table 3). A rough scaling of the ratio of vertical to horizontal viscosity, assuming the minimum horizontal viscosity imposed by the numerical resolution of the WBC (physical values would be much lower though) and a typical vertical viscosity in the ocean interior, gives:
![]() .
.
The results (exp. 2 and 3) confirm the validity of the PG dynamics for these mid-latitude coarse-resolution simulations (Weaver and Sarachik, 1991). In fact, the difference in the coding of the PG dynamics from the B-grid to the A-grid formulation using Laplacian viscosity and no-slip boundary conditions is more important than the effect of the non-linear terms (exp. 2, 3 and 4).
b. Various parameterizations for Reynolds stress and lateral boundary layers
Zhang et al. (1992) used the PG equations with no explicit friction in the interior (except for the barotropic wind-driven circulation) and no-slip boundary conditions (model PG0 here). In comparison to the Bryan-Cox PE model used at coarse resolution under restoring boundary conditions and wind forcing, their simple PG model produced comparable currents and thermocline depth, even though they employed higher vertical diffusivity and lower horizontal resolution in the PE model. This was interpreted as a consequence of the large eddy viscosity in the PE model, although we find different results in our comparison using the same geometry, resolution, parameters and forcing (section 3d). Even with no friction added to satisfy the transfers from potential to kinetic energy, the numerical results are reasonable. Zhang et al. (1992) also analyzed the influence of adding linear friction in the baroclinic momentum equations (model PGR hereafter).
Colin de Verdière (1988, 1989) used this set of equations with horizontal Laplacian viscosity to check the Sverdrup balance in a thermally driven case; wind stress was added later to study the non-linear interaction with the thermohaline component of the circulation. This model (PGLA hereafter), coded on an A-grid and solving the horizontal velocity field in spectral space, is used here to validate the B-grid code (PGL, consistent with the MOM grid) and to evaluate the effects of the horizontal grid on the results.
Winton (1993) used linear friction as well as Laplacian friction in similar mid-latitude simulations to examine centennial thermohaline oscillations. When horizontal linear friction was used with no-normal-flow boundary conditions, the tangential velocities along the boundaries were determined using the frictional vorticity equation applied to the center of boundary grid-boxes (Winton, 1993–model PGRW hereafter). This original closure, where the boundary condition is applied to the vorticity instead of the momentum equations, is implemented here to provide an alternative to the traditional no-slip and free-slip boundary conditions (both break the rotational constraint on horizontal divergence). Winton and Sarachik (1993) did not analyze in detail the discrepancies induced by their original boundary layer scheme but instead concentrated on the mechanism of the thermohaline variability; we pursue this work through a specific comparison of the influence of these parameterizations.
Salmon (1986, 1990) showed that the use of linear friction in three dimensions results in a well-posed set of equations only if the hydrostatic approximation is relaxed. With a linear equation for the tracers as well, he analytically found the important physical features of traditional models (mainly the scaling of coastal boundary layers), although the lateral non-hydrostatic boundary layers were too narrow to be resolved explicitly. He showed some thermocline simulations in his latter paper, but did not apply realistic forcing over a whole ocean basin. Here, we implement this non-hydrostatic set of equations (model PGRS) and observe a tendency towards convergence to Winton’s closure when the friction coefficient in the vertical momentum equation approaches zero (exp. 14 to 16 in Table 3).
Samelson and Vallis (1997a, b) proposed an interesting alternative to relaxing the hydrostatic approximation within linear friction by adding biharmonic diffusion for tracers, whose coefficient was chosen to reduce diapycnal fluxes in the WBC (model PGR4 hereafter). The balance between harmonic and biharmonic tracer fluxes across the lateral walls provided the additional boundary condition to define the along-shore tracer transport. Note that the implementation of this model requires a tracer equation slightly different from the others through the addition of biharmonic diffusion, which induces the formation of significantly warmer deep waters.
In order to compare these various parameterizations for momentum dissipation and lateral boundary layers, we consider a modular program iterating the tracer evolution by advection, diffusion and convection, using the traditional energy-conserving schemes in relation with the hydrostatic pressure formulation on a B-grid (Bryan, 1969; Semtner, 1986). The vertical velocity field is computed from the continuity equation at the interface between the model levels. Pressure and temperature are defined at mid-levels in the centers of the model grid boxes while horizontal velocities are defined at the corners (same level). Tables 1 and 2 summarize the different combinations of momentum dissipation and boundary conditions compared in the next section (the letter 'L' is used for Laplacian viscosity while 'R' refers to linear Rayleigh friction), while the Appendix describes their numerical implementation.
c. A scaling for the vertical velocities in various lateral boundary layers
The choice of the viscosity coefficient for the Laplacian operator is dictated by the need to resolve the Munk boundary layer for vorticity dissipation: AH┼2 b Dx3. The geostrophic balance then holds even close to the boundaries, as shown by the horizontal Ekman number: E=AH/(fDx2)=2bDx/f┼2Dx/a┼0.06 (where a is the Earth’s radius). The traditional no-slip boundary condition forces the horizontal velocities to vanish at the boundary, which provides a simple scaling for the vertical velocities using the horizontal velocity scale for the flows impinging into the coast: w=O(UDz/Dx)┼(1 cm s-1´ 100 m)/160 km┼10-5 m s-1, i.e. vertical transport of the order of 0.2 Sv (1 Sv║106 m3 s—1) in each gridbox along the boundaries. This scaling also applies to PG0 and PGR. Note that free-slip boundary conditions do not alter this scaling (cross-shore derivative of along-shore velocity does not appear in the continuity equation) unless along-shore variations of along-shore velocities become significant.
Frictional vorticity closure, on the other hand, does profoundly influence the continuity equation along the boundaries. Using Rayleigh friction (given the choice of the linear coefficient to resolve the Stommel boundary layer, eH┼2 b Dx), the Ekman number (E=eH/f) is of the same order as with Laplacian viscosity. However, Winton’s closure for the tangential velocities forces a different scaling from the continuity equation:
![]() .
.
One can see this vorticity constraint as a consequence of a baroclinic instability cascade occurring in lateral boundary layers (Csanady, 1989). However, we don’t try further to justify such a crude closure but rather look at its consequences for the thermohaline circulation.
d. Model geometry, parameters and forcing
The Cartesian, b-plane, centered at 40°N, extends 4480 km from 20°N to 60°N, and 5120 km (roughly 60°) in longitude. The horizontal resolution is 160 km and the depth of the basin is 4500 m, discretized by 15 levels (respectively 50¥3, 100, 150, 200, 250, 300, 350, 400, 450, 500, 550¥3 m deep). Only PGRS differs with 6 times more vertical levels, all of uniform 50 m depth. The uniform tracer mixing coefficients are typical for the resolution, with the horizontal and vertical eddy diffusivities respectively set at KH=700 m2 s-1 and KV=10-4 m2 s-1. This latter value is larger than measured in the interior of the ocean and is required to obtain a reasonable overturning O(10 Sv) within a basin much smaller than the actual upwelling area of deep water formed in the North Atlantic. A convection parameterization (Rahmstorf, 1993) is included to remove all static instabilities at each time-step. The momentum dissipation coefficients are derived from the scaling of the boundary layers for each parameterization: AH=1.5¥105 m2 s-1 with Laplacian friction and eH=4.4¥10-6 s-1 with linear friction. For PGRS, different values of the vertical friction coefficient eV are used (8.85 and 88.5 s-1, equivalent to 0.03 and 0.3 in the scaling of the hydrostatic equation).
The atmospheric forcing consists of restoring the sea surface temperature to zonally-uniform reference temperatures, linearly decreasing from 25°C at 20°N to 2°C at 60°N. The restoring time scale is based on Haney (1971) estimated fluxes of 35 W m-2 K-1, equivalent to a 66 days restoring time constant for the 50 m deep mixed layer. Additional tests with fixed flux (Neumann) and fixed surface temperature (Dirichlet) boundary conditions indicated our conclusions on the effects of momentum dissipation and lateral boundary layer parameterizations are only slightly affected by this choice. We present the results from the experiments with restoring boundary conditions since they are the most commonly used in ocean models: these experiments lead to a steady-state solution with realistic surface fluxes (fixed heat fluxes usually drive decadal oscillations, while Dirichlet condition induce unrealistically high surface fluxes in the Gulf Stream region).
e. Preliminary grouping of the models and their results
Starting from an initial uniform temperature of 4°C in the basin, we ran the models to a steady state (3000 years) by which time the residual surface heat flux varied between 10-3 and 10-5 W m-2. PGL, PGLA and the MOM are virtually identical since they implement the same dissipation scheme: they will serve as our reference for the comparison. Through the analysis of global diagnostics as well as more detailed patterns, we found a large dependency in the results for different dynamical boundary conditions. With reduced vertical transports along the boundaries, PGRW, PGR4 and PGRS show striking similarities when compared to other models. The comparison of the results from these two groups leads the discussion: the former represents the traditional PE models at coarse resolution with no-slip boundary conditions, the latter being an alternative emphasizing horizontal instead of vertical recirculation along the boundaries, via tangential velocities along the lateral walls.
3. The Veronis effect and the efficiency of the thermohaline circulation
a. The mean circulation
After an energetic spin-up of about 30 years, the mean circulation slowly settles into a steady-state on diffusive time scales. For all the models, the main features are in fair agreement with theoretical expectations given the forcing: the meridional temperature gradient drives an eastward zonal jet in the upper layers (reversed at depth for zero barotropic transport), that is shifted to the northern part of the basin (Fig. 1). This jet is fed by the WBC, originating from a weaker westward jet at low latitudes (isotherms rise upward towards the tropical boundary) and the boundary upwelling with varying proportions according to the chosen lateral boundary layer parameterization. Deep-water is formed along the northern boundary where convection takes place, but most of the deep vertical mass transport occurs in the north-east corner. Upwelling regions are along the western boundary and in most of the interior (Fig. 2), in agreement with the hypothesis of the Stommel-Arons (1960) theory. Abyssal waters have a weak northward motion in the interior, but the most significant part of their flow is westward (eastward) along the northern (southern) boundary, and southward in the deep western boundary undercurrent. In the absence of denser waters from the other hemisphere, the stratification is very weak at depth. The circulation is split into 2 layers, showing an anticyclonic (cyclonic) gyre in the upper (lower) layer, the flow being primarily horizontally divergent in each layer. With a uniform vertical diffusivity and no seasonal cycle, the thermocline is defined by the inversion of horizontal currents rather than by the sharpest density gradient (this is also where the largest vertical velocities occur): most of the density profiles are exponential with height except where convection occurs. The western intensification is not only due to the b-effect (since it is still present on an f-plane) but also to the different efficiency of convection and vertical mixing processes affecting the upper layer anticyclonic circulation, as discussed by Colin de Verdière (1988) and Duffield (1993).
As shown in Fig. 1, the differences in the horizontal circulation for the various models occur principally close to the boundaries. While PG0 is very similar to PGL in the north-east corner, PGRW departs fundamentally with northward-curving isotherms. This is due to the horizontal recirculation of the eastward jet impinging into the eastern boundary, in sharp contrast with the vertical dissipation of this jet within no-slip boundary conditions. In addition, westward velocities along the northern boundaries produce a limited subpolar gyre, whose similarity to observations (McCartney and Talley, 1982) was discussed by Winton and Sarachik (1993). These boundary velocities are responsible for the westward shift of the coolest region from PGL to PGRW. The dynamics of the WBC also shows significant discrepancies: PGL illustrates the traditional overshoot associated with Laplacian dissipation (Munk, 1950), and recirculation on the east side of the current (Masuda and Uehara, 1992). The models with linear friction lack these features: they produce a weaker northward transport of mass (10 to 12 Sv, column 9 in Table 3), consistent with the differences in the wind-driven barotropic circulation between Stommel (1948) and Munk (1950) solutions. Consequently, the WBC has a much broader and diffuse signature, in terms of temperature, with linear friction than with Laplacian viscosity. As a bias of the numerical boundary layer, the WBC in PG0 is limited to one grid point but achieves a northward transport larger than PGL (19 vs. 15 Sv). Finally, the no-slip boundary condition along the western boundary induces cold water in this region, brought by a large upwelling that is much reduced in PGRW: this will be discussed in detail in section 3c.
b. The geostrophic and Sverdrup balances
Although the dynamics of the lateral boundary layer significantly influence the mean circulation, the interior velocities remain principally in geostrophic balance. As a consequence, we expect the Sverdrup balance to hold as well. Colin de Verdière (1988) showed a relatively good agreement for the Sverdrup balance (within 50% accuracy) and Stommel-Arons's type of deep circulation in the heated region of the basin. As shown in Fig. 2, the upwelling at the base of the thermocline is quite similar for all the models in the southern half of the basin, varying between 4.4 and 5 Sv. It differs greatly along the boundaries and in the northern regions.
Here we check the accuracy of the geostrophic and Sverdrup balances in the various models. As an alternative to the horizontal maps presented by Colin de Verdière, we simply plot the percentage of the volume of the basin that satisfies each balance as a function of the tolerance (Fig. 3). For the geostrophic balance, the relative error is computed as the norm of the vector difference between the Coriolis force and the pressure gradient, divided by the mean of the norms of the 2 vectors (given the location of pressure and velocities on the B-grid, only interior velocity points are considered). For the Sverdrup balance, it is the absolute difference between (b v) and (f wZ) divided by the mean of the 2 positive values (for the interior B-grid tracer points only).
PG0 is the best a purely geostrophic numerical model can do: the geostrophic balance is satisfied by 100% of the interior points, but the Sverdrup balance is not perfect because of numerical issues (only 80% of the domain satisfies a 10% tolerance). Laplacian dissipation is satisfying in terms of geostrophy: 70% (90%) of the domain satisfies a 2% (5%) tolerance, but is far worse than PG0 for the Sverdrup balance: only 20% of the domain is within a 10% tolerance. Linear friction is the worst: the friction coefficient acts as a cut-off, since none of the domain satisfies the geostrophic balance within a 3% accuracy. The satisfaction density increases slowly to 60% (100%) for a 5% (8%) tolerance. In terms of the Sverdrup balance, the accuracy is disastrous, barely better than the probability of tolerance satisfaction for random numbers (shaded in Fig. 3b). This is due to the weak scale selectivity of the linear friction. Scaling arguments in the vorticity equation determine the choice of the friction coefficient so that the dissipative boundary layer would be resolved within a few grid-points. The emergence of the Sverdrup balance in the remainder of the basin requires a strong reduction of the dissipative term outside the boundary layers and linear friction obviously lacks this ability.
Of course, the choice of the friction coefficient is critical for these performances, although the horizontal resolution needs to be changed accordingly to resolve the western boundary layer. Doubling the horizontal resolution and using a linear friction of 2% of the rotation rate of the earth (1.46´ 10-6 s-1) greatly improved the Sverdrup balance accuracy within the Rayleigh friction models, far above the significance level. Clearly, the accuracy of the Sverdrup balance relies on a very accurate geostrophic balance: only the regions where the latter is verified within less than 1% tolerance can qualify for the former. The geostrophic balance is accurately satisfied in all these models, but the Sverdrup balance is not: it requires the friction terms to be negligible in the interior, while of order 1 in the dissipative boundary layer. The scale-selectivity of the momentum dissipation operator is crucial: Higher order operators (Laplacian, biharmonic) are required for a good accuracy of the Sverdrup balance. Note that the choice of boundary conditions is almost indifferent to these balances as they are dominated by the evaluation at interior points.
c. Vertical velocities and overturnings
The meridional and zonal overturning streamfunctions (MOSF and ZOSF hereafter) are defined as the vertical integration of the zonally- (meridionally-) averaged northward (eastward) velocities:
![]() ;
; ![]() .
.
These diagnostics are certainly among the most sensitive to the choice of parameterizations in our experiments. The MOSF (Fig. 4, Table 3) varies from 7.6 Sv in PGRS to 15.6 Sv for PG0. These mass transports show the greatest sensitivity to the lateral boundary layer parameterization (PGRW vs. PGR), not to the momentum dissipation scheme (PGL vs. PG0). The frictional closures for tangential velocities within no-normal-flow boundary condition generate a MOSF below 9 Sv, the free-slip one with harmonic or biharmonic viscosity, around 11 Sv, and the no-slip one, above 14 Sv (whatever internal dissipation is chosen). The contribution of the western upwelling to the meridional overturning reaches 5 to 6 Sv for PGL between 850 and 1900 m deep (where the MOSF is maximum), but 10 to 12 Sv for PG0 and only 1 Sv for PGRW. Comparing the northward volume transport achieved by the WBC in the different models and the latitude of its maximum (columns 9 and 10 in Table 3), we found a good correlation with the MOSF in most of the cases, which confirms the schematic thermohaline loop where the WBC brings the water that will sink in the northern regions and feeds the deep WBC. However, the WBC transport is not always larger than the overturning, as suggested by Stommel-Arons dynamics where the meridional interior circulation is opposed to the WBC.
We observe the same variability in the ZOSF (Fig. 5, Table 3), showing the general pattern of two loops, one concentrated at the surface and extending along the western boundary, the other deeper along the eastern boundary. Both are associated with upwelling along the meridional borders, especially the amplitude of the zonal overturning which is almost entirely set by the maximum upwelling along the western boundary. These two loops differ significantly in intensity and spatial distribution according to the boundary conditions employed: The eastern deep cell transports 2 Sv in PGRW and fills the whole width of the basin, but 4 Sv in PGL where it is deeper and restricted to one third of the basin longitudinally. In agreement with the thermal wind balance, these patterns are coherent with the north-south density gradient, which is negative only in the regions where the ZOSF is negative. The surface loop is even more variable, driving 2 Sv in PGRW (near the surface) and up to 8 Sv in PGL and 12 Sv in PG0 (extending to the bottom of the western half of the basin). The ZOSF is thus extremely sensitive to the parameterization of lateral boundary layers.
The closure of lateral velocities along the boundaries, whose divergence feeds the vertical velocity field, largely influences the overturning, since the divergence of horizontal flows in the interior (and hence the generation of vertical velocities) are limited by the rotational constraint. In Fig. 6 we examine the vertical velocities along the boundaries at the base of the thermocline in different models. The vertical velocity field in PGRW is very weak, regular and smooth, in comparison with the large values and variability in PGL (these values and variability are even larger in PG0). Although the mean vertical velocities in the interior are similar in all models (of the order of 5´ 10-7 m s-1, see Fig. 2), mean vertical velocities reach more than 10-5 m s-1 along the boundaries in PGL and PG0, i.e. more than 20 times the interior average velocities. The total vertical transports occurring along the boundaries are accordingly large (around 30 Sv for PGL and 40 Sv for PG0 at a depth of 2000 m, compared to 12 Sv peaking at 700 m for PGRW). In the north-east corner, downwelling in PGL and PG0 sums up to a few Sverdrups and contributes significantly to the MOSF and ZOSF intensity, but also to the heat budget of the deep water (in spite of the weak vertical gradient of temperature in this region). The vertical velocities along the western boundary differ by almost an order of magnitude from PGRW to PGL or PG0, as expected from the scaling based on the lateral boundary layer parameterization (section 2c). The net upwelling integrated along the western boundary (given in column 13 of Table 3) reaches 6 Sv (at a depth of 850 m) in PGL, 12 Sv in PG0, but less than 2 Sv (maximum at 250 m) in PGRW.
This feature is often related to the Veronis effect (1975–see section 5b): large vertical velocities (transporting heat downward) balance the strong horizontal diffusion of heat across the steeply sloping isopycnals in the Gulf Stream. Veronis’ analysis of Holland’s (1971) numerical experiments pointed out large upwelling in the WBC (due to the large horizontal diffusivity) as the cause for the general downwelling at the base of the thermocline, in contradiction with Stommel-Arons (1960) theory based on the net upward flow at the base of the thermocline (balancing the deep-water formation). Masuda and Uehara (1992), Gough and Welch (1994) and more recently Lazar et al. (1999) related this downwelling, both analytically, statistically and numerically, to the horizontal mixing of tracer. Indeed Holland resolved this problem in a later experiment by reducing the horizontal diffusivity from 5000 to 3000 m2 s-1. Even with the low value we use here (700 m2 s-1), the western upwelling remains large in PGL and PG0, while most of the interior still shows upwelling in agreement with southward flow at depth through the Sverdrup balance. These vertical velocities surely decrease the efficiency of the thermohaline circulation in two ways: by pumping cold water out of the deep WBC into the WBC ("shortcut" for the deep water path), and by producing deep waters by downwelling in the north-east corner that warm the waters formed by deep convection in the cooler mid-northern regions. Finally, the higher mass transports caused by this WBC upwelling and north-east downwelling are associated with the warmest bottom waters and lower poleward heat transport.
Figure 7 shows latitude-depth sections of the zonally averaged temperature in the thermocline. Straub (1996) points out that this field should not be very sensitive to the internal dynamics of the model, since the boundary currents concern only a small ratio of the basin area. In fact we find some noticeable discrepancies regarding the deep and thermocline waters temperature. The main effect we attribute to the dynamics is to set the bottom water temperature and hence the temperature at the base of the thermocline (since the deep waters are very weakly stratified). The dynamics also plays a significant role in the cross-isopycnal mixing through upwelling and downwelling along the boundaries.
Mean basin, mean bottom and minimum temperatures are highly correlated in all the models (Table 3, Fig. 9a): in steady state, the cancellation of the area average of the surface heat flux requires that the mean surface temperature equals the mean restoring temperature, i.e. 13.5°C for these experiments. The coldest temperatures reached at the surface slowly fill up the whole deep basin through convection, followed by deep advection, establishing the bottom distributions. The lowest temperatures occur along the northern boundaries (where the restoring temperature is the coolest), usually in the western half of the basin, as a balance dominated by north-south diffusion, surface forcing and convection. Significant differences are achieved by the different models in terms of bottom water temperature. The PGRW group produces the lowest values (~ 3.4°C), PG0 the highest (3.75°C), the Laplacian models being in the middle (~3.54°C). At depth, PGL has a much larger range of temperatures than PGRW (0.036°C standard deviation compared to 0.008 for the 4225 m deep level), since the waters driven by the downwelling in the north-east corner are 0.2°C warmer than the ones formed by convection along the northern boundary, close to the north-west corner. The change in the lateral boundary layer parameterization appears to be the most influential, as the interior dissipation accounts for only 0.05°C change from PGR to PGL or from PGLslip to PGBslip, as long as it is not purely geostrophic (PG0 differs from these by 0.3°C).
We suggest that the strong vertical transports along the boundaries, decoupled from static instability areas, explain a large part of the discrepancies in the bottom temperatures. Indeed the convective regions are the ones with the coldest temperatures at the surface. If the downward velocities occur in the same area, the deep waters are fed by the coldest surface waters; if strong downwelling occurs elsewhere, deep waters result from a mixing of water cooled by convection and water advected vertically from the surface. This induces bottom temperatures that are higher than what can be expected from the first process only.
Finally, the PGRW group has the sharpest thermocline, while PG0 has the most diffuse (this is even more clearly represented by the zonally averaged Brunt-Väisälä frequency, not shown). This latter conclusion disagrees with Zhang et al. (1992), who found a sharper thermocline in the purely geostrophic model than in the MOM, for a slightly different configuration. We do not observe the significant difference in the meridional overturning between PG0 and PGL that support their explanation, although it is supported in terms of cross-isopycnal transports (the maxima of the cross-isopycnal overturning streamfunction are respectively 11.2 and 13.1 Sv for PGL and PG0). Since their conclusion holds with no wind forcing, we must consider the influence of the horizontal grid or the details of the coding (D-grid in their model, S. Zhang personal communication). The upwelling along the western boundary is twice as strong in PG0 than in PGL, even in terms of diapycnal upwelling. The more diffuse thermocline in PG0 appears as a consequence of intensified vertical mixing by upward and downward motions, in relation with the higher bottom water temperature. Since the vertical transports occurring in the interior are of the same order of magnitude among the models, the enhanced vertical mixing is due to the vertical transports in the lateral boundary layers, while the momentum dissipation scheme, influencing the horizontal divergence in the interior, has almost no effect unless it is absent as in PG0.
At equilibrium, we integrate vertically and zonally the tracer equation to determine the contribution of the advective and diffusive heat transports in balancing the surface heat flux. By integrating from the southern boundary (where no flux occurs) to any latitude, we compute the advective and diffusive poleward heat transports, whose sum is the total ocean heat transport (equal to the integrated surface heat fluxes in steady state):
![]()
![]()
![]()
This represents the efficiency of the ocean in transporting heat northward, but depends on the surface forcing (the choice of restoring surface boundary conditions and the associated relaxation time scale). The diffusive PHT shows a strong sensitivity to the horizontal diffusivity (representing the non-resolved eddy-induced heat transport, less than 10% of the total here) while the advective part follows a geostrophic scaling strongly influenced by the vertical diffusivity (Bryan, 1987; Colin de Verdière, 1988; Bryan, 1991), setting the thermocline depth and providing the potential energy to the whole system in the absence of wind forcing. The actual role of the ageostrophic dynamics of the ocean is thus not trivial to foresee. In fact, the maximum advective heat transport varies by less than 15%, from 0.21 PW (1 PW║1015 W) for PG0 to 0.24 for PGRW (Table 3). Such a narrow range of variation is surprising given the large deviations observed in the meridional overturning, suggesting a potential bias by the surface forcing. Furthermore, the models with the largest overturning have the weakest PHT. In the next section we investigate the relationship between the meridional overturning and the thermohaline efficiency in transporting heat poleward.
f. The thermohaline efficiency
The amount of heat the thermohaline circulation transports poleward might crudely be estimated as the product of the overturning rate and the temperature contrast between poleward flowing thermocline water and equatorward flowing deep water: PHT µ r0 CP ´ MOSF ´ DT. We now test the relevance of such a simple scaling for our models. Zonally-averaging our ocean, we find a thermocline with northward velocities generally in the first 800 m and deep water with southward velocities below, as observed in the WBCs. The PHT of such a simple 2-layer model is proportional to the transport and the temperature difference between the upper and the lower branch. DT is estimated as the difference between the mean thermocline temperature (around 9°C) and the mean bottom temperature (around 4°C). This gives a reasonable estimation of the PHT: 4¥106 J m-3 K-1 ´ 5°C ´ 10 Sv = 0.2 PW.
To assess the relevance of our simple relationship, we examine the maximum advective PHT as a function of MOSF and DT, varying as the opposite of the mean bottom temperature (the sensitivity to the thermocline temperature is biased by the restoring surface boundary condition that imposes a 13.5°C mean surface temperature at steady state), for the different models. Although the correlation with MOSF (Fig. 8a) is better than with the bottom temperature (Fig. 8b), both are negative. From the last formula, we were expecting the opposite correlation between PHT and MOSF. But considering the strong correlation between MOSF and mean bottom temperature for all the models (Fig. 8c), it appears that the shallow to deep water temperature contrast controls the PHT in spite of the change in the overturning rate. In analogy with electricity transport in wires (intensity┼overturning), the higher the voltage (DT), the lower the loss of energy. And it is the overall efficiency of the thermohaline loop that enables the ocean to transport heat poleward.
These results suggest that the thermocline to deep water temperature contrast is more important than the overturning intensity in controlling the poleward heat transport. Both should be considered when assessing a global model’s efficiency to transport heat poleward. Finally, we look at the correlation between the western upwelling (as a measure of the Veronis effect) and the deep water temperature (Fig. 8d): The excellent correlation clearly shows that the shortcut of the thermohaline loop (via upwelling in the Gulf Stream between 40-60°N) does primarily influence the deep water temperature and consequently the whole thermohaline efficiency (Böning et al., 1995).
Following Colin de Verdière (1988), we compare the potential energy balance for each models’ steady state. The objective is to evaluate the dissipation rate associated with the choice of momentum dissipation and boundary conditions, and their consequences on the global balance. Finally we define a thermodynamic efficiency that compares well with the previously estimated one based on the poleward heat transport and the deep water temperatures.
a. The potential energy balance
The potential energy equation, resulting from the basin integration of (g z) times the density equation, leads to the balance between a source term related to the vertical mixing, two sinks from the convection and the momentum dissipation, and a residual term from the surface fluxes, which tends to zero at steady state. These terms have the following expressions (in W m-2), with A being the total surface area of the ocean basin:
![]() ,
,
![]() .
.
where Conv(x,y,z) is the interior redistribution of density necessary to remove static instabilities (r0 a times the Convection term in the temperature equation in section 2a). Note that this value does not depend on a reference level since: ![]()
The dissipation term is computed from the cross-correlation of vertical velocities and density, in order to use the same formula whatever momentum dissipation scheme is used:
![]() .
.
The residual term from the surface heat flux (depending on the reference level) is always negligible after 3000 years. We simply measure the residual surface heat flux:
![]() .
.
In addition, we compute the kinetic energy (KE) in different ways according to the numerical grid: on an A-grid, the velocities are weighted by the volume of the surrounding grid-box, but on the B-grid, either an average over the 4 corners is done, to mimic the A-grid calculation, or the boundary values are weighted by one half of the volume of the grid-box. These two methods lead to significant differences which enlighten the important contributions of the velocities along the boundaries to the total KE:
![]() .
.
The available potential energy (APE further) is also computed in two different ways. The first method follows Oort et al. (1989) and measures the departure of the isopycnals from a reference state defined as the horizontal mean of the densities. The second method uses a more accurate but computationally intensive procedure, although in our study it is easily implemented due to the linear equation of state and the box geometry. The reference stratification is determined by successively tracking the coldest grid-boxes in the basin and summing up their volumes to fill the basin layers, starting from the bottom. This gives a mean temperature for all the levels through an adiabatic redistribution of the ocean elements conserving their volume and temperature. The APE is then computed as the difference between the initial potential energy and the potential energy of the horizontally uniform reference state (the arbitrary reference height does not influence the result given the identical thermal content of the two states). Comparison of the two methods shows the uncertainty in the determination of the APE in the ocean. Although the order of magnitude is fairly similar, the ordering of the models is not always the same, and the range of variation of APE using the second method is much smaller than with the first one (first order linearization):
![]() ,
,
![]() .
.
b. Comparison of the energy balance for the different models
As expected from the variations in bottom water temperature, the energy diagnostics in Table 4 show large variability in the APE according to the dynamical closure. The PGRW group achieves the lowest values, increased by a factor of 2 to 4 (depending on the formula used) for Laplacian friction or no-slip boundary conditions. The purely geostrophic model yields the highest APE. Understanding the ordering of APE for the different models is not trivial, as it is the opposite of the surface to bottom density contrasts which controls the reference stratification potential energy. The ordering seems correlated with the variability in the temperature field, usually dependent on the diapycnal velocities along the boundaries.
The kinetic energy (KE) interpretation is complicated by the two formulations: the B-grid value, when available, is always bigger than the A-grid one, as the averaging smoothes the largest velocities. The discrepancy between the two values is rather large when no-slip boundary conditions are used, as the vorticity closure (or non-hydrostatic with small vertical friction) generates high tangential velocities at the boundaries. Thus, a major part (60% at least) of the KE in the PGRW models comes from the boundaries, while the interior velocities are weaker than in PGL. When no interior dissipation is used (PG0), the highest KE is achieved. In this case only, the use of frictional vorticity closure (PG0W) to solve for lateral velocities with the no-normal-flow boundary condition introduces some dissipation and reduces the energy of the steady state. Using the same boundary condition, linear friction always induces a significantly lower KE than Laplacian viscosity.
The term arising from the surface flux in the potential energy equation is usually less than 10-4 W m-2 after 3000 years of integration, inducing an accurate balance between the other source and sink terms. The only source term for potential energy is that through vertical mixing, which we find comparable amongst the closure schemes. This is related to the similarity of surface to deep water characteristics in each model. Since the mean surface temperature needs to match the mean restoring temperature (13.5°C) at steady-state, the relative variation of this source term is easily predicted from the variability of the mean bottom temperature (3.5▒0.2 °C) over the surface to bottom difference (~10°C), i.e. a few percent change.
The comparison of the sink terms is more interesting since various distributions between convection and dissipation occur. First, PG0 shows an extreme case where the vertical mixing source is entirely dissipated by convection: purely geostrophic velocities do not produce any work and the imposed no-slip boundary condition satisfies a zero net dissipation (Bryan, 1969; Colin de Verdière, 1988). In the Laplacian cases, convection is a sink that is twice as important as momentum dissipation, which even reduces with lower viscosity (this is not changed by free-slip boundary conditions). The linear friction model with no-slip boundary condition, PGR, is very similar, with 15% more dissipation and consequently lower convection. On the other hand, the PGRW group looses potential energy mainly through KE dissipation (twice as important as convection). A tentative interpretation is that the vertical velocity field in these models efficiently moves the coldest water downward, having the same effect as convection (the more important rate of dissipation of energy is consistent with the lower KE with linear friction). A crude evaluation of this is possible with linear friction (as 2 eH KE) for PGR or PGRW (and PGRS with low vertical friction), and this compares to the model dissipation depending on which scheme is used to compute KE. Increasing the vertical friction coefficient in PGRS makes the part of the dissipation of vertical kinetic energy more significant, reaching 10% of the horizontal one for eV=88.5 s-1 (0.3 when scaled). The type of boundary condition proves itself important again through its influence on the vertical velocities along the boundary. We already measured the influence of the shift from a no-slip to a no-normal-flow boundary condition with Rayleigh friction, inverting the ratio of convection to dissipation PE depletion.
Comparing PG0 and PG0W is more striking, as the frictional vorticity closure for the lateral boundaries is enough to get a convection-dissipation ratio identical to PGRW. Even with no interior dissipation, the tangential velocities and associated vertical velocities along the boundaries reduce the role of convection by 60%. Were our models able to resolve the Rossby radius of deformation, the reduction of the convective adjustment contribution would acknowledge the good performance of the model in producing the right vertical velocities to resolve convection instead of parameterizing it. Unfortunately, at coarse resolution, this argument is no longer relevant to draw conclusions on the performance of the models.
For comparison purposes, Fig. 2 presents the vertical transports at 850 m (the base of the thermocline) and the convection region across this level for PGRW and PGL. Obviously, PGRW achieves a nice agreement between downwelling and convection in the northern regions, as opposed to PGL where the noisy vertical velocity field is rarely associated with convection. Comparing the deep convection regions (Figs. 2, 4 and 5) shows an area of the northern boundary 3 times larger in PGL than PGRW, where convection is more concentrated in the western part as a consequence of the westward velocities along the northern boundaries. The north-east corner shows more convection in PGL as the large eastward current drives all the surface water there.
The high-resolution non-hydrostatic simulations of Send and Marshall (1995) show that a good agreement between convection regions and large-scale downwelling velocities is not necessary since convective plumes transport properties by turbulent mixing without significant net mass transports. Heat transfers by convection do not directly appear in the MOSF, although they modify the properties of the deep waters and aid in setting up east-west pressure gradients which ultimately drive the overturning.
c. A thermodynamic thermohaline efficiency
From a thermodynamical point of view, we can define the efficiency of the thermohaline circulation as the ratio of the work produced by the heat input. The work produced is simply the rate of dissipation (and production) of kinetic energy previously defined (column 8, Table 4), while the heat input is evaluated here as the total positive (or negative) integrated heat fluxes at the surface divided by the basin area (column 9). The ratio agrees well with our estimation of the efficiency of the thermohaline circulation through its poleward heat transport and its ability to produce cool deep waters. The later is particularly relevant when looking at the maximum efficiency of a Carnot heat engine operating in a closed cycle between a cold and a warm heat source, which is maximized (but still lower than 7%) when the temperature difference is the largest (Colin de Verdière, 1992).
a. The Veronis effect revisited
With the exception of the tangential velocities along the lateral walls, the dynamical balance in the interior of the basin is geostrophy and the effect of momentum dissipation remains fairly small. Hence, most of the differences we observe in the interior dynamics are due to changes in the temperature field. In order to properly compare the velocity fields associated with each lateral boundary layer parameterization we compute their diagnostic PG dynamics for the same temperature field, constructed as an average of the steady-state temperature fields of the 16 models summarized in Table 3. The results confirm the high reliability of geostrophic balance in the interior of the basin whatever the model. However, dramatic differences occur along the boundaries: the strong horizontal tangential velocities from the frictional closures in models using no-normal-flow boundary conditions have no counterpart in models with no-slip boundary conditions, while the vertical velocities are totally the opposite from one group to the other (with almost an order of magnitude difference). These astonishing differences are much stronger than in each model’s steady state and prove that the boundary conditions are responsible for producing the large differences in the final steady-state temperatures.
This suggests that the vertical velocities arising from the boundary condition initiate the process of increasing the slope of the isopycnals and consequently the Veronis effect. In steady state, we compare the tracer balance terms along the western boundary in the different models. For PGL, the vertical tracer advection is the most important term in the balance (reaching 7 K y-1 at 200 m), while the horizontal diffusion is 2 or 3 times smaller (hardly reaching 2 K y-1). The imbalance is even larger with PG0, while for PGRW, the vertical advection terms reach 5 K y-1 vs. 1 K y-1 for the horizontal diffusion. If the whole balance was displaced by the cross-isopycnal horizontal diffusion, these terms would likely be the largest. Since the vertical advection term is much larger, it must be the dynamics that induce the large upwelling and consequently the Veronis effect. The lateral boundary conditions are then responsible for the upwelling, whether the diffusion is horizontal or isopycnal. We investigate this last point in the next paragraph.
b. Sensitivity to horizontal or isopycnal diffusion
We observed that the horizontal diffusivity is an important parameter influencing the minimum surface temperature achieved at the surface in these models, and thus the mean basin and bottom temperatures. A striking linear relationship exists between these values and the horizontal diffusivity in a log-log plot, especially for PGL (Fig. 9a). For PGRW, two regimes with different slopes seem to occur below and above 700 m2 s-1, the latter one being very similar to PGL. Bryan (1986) concluded that the sensitivity to KH is due to its effect on cross-isopycnal mixing, and as such, an artifact of the horizontal instead of isopycnal formulation. However, the very different sensitivity of the upwelling along the western boundary in PGL and PGRW with KH (Fig. 9b) suggests that the dynamics of the model is equally important in controlling the upwelling.
We implemented isopycnal mixing in MOM to evaluate the implied modifications on the temperature field (90 levels of 50 m were used on the vertical for numerical accuracy): the bottom waters cool to 3.10°C (vs. 3.60°C originally for MOM with 90 levels) but a background horizontal diffusion of 100 m2 s-1 is required for numerical stability. Note that the background diffusion is really the only one that matters since isopycnal diffusion with a single tracer in the linear equation of state corresponds to no diffusion at all. The addition of the Gent and McWilliams (1990) parameterization for mesoscale eddy-induced tracer transport (isopycnal thickness diffusion of 700 m2 s-1) allows us to eliminate the background diffusivity and the mean bottom temperature cools further to 2.85°C (3.28°C with horizontal mixing instead of isopycnal mixing).
The mean basin temperature varies by 0.5°C depending on the momentum dissipation and lateral boundary layers parameterization, as much as the change induced by changing the eddy mixing from horizontal to (quasi) isopycnal in the MOM, or by changing the horizontal mixing coefficient within its range of uncertainty in PGL or PGRW. This significant influence justifies a posteriori our study.
c. Relevance of the large upwelling in the western boundary current
We confirm herein the conclusions of Huang and Yang (1996) that upwelling within the WBC is a substantial part of the basinwide budget. Through a 2-level analytical model, they showed that linear friction induces a contribution to the vertical velocity that is dominant in the WBC and towards upwelling. Our results suggest that it is not specific to linear friction, but applies to Laplacian viscosity, to biharmonic viscosity and to the no-friction case as well, when using no-slip boundary conditions. Huang and Yang found the strongest upwelling along the western boundary, but consider it is a necessary feature of frictional western boundary layers. Their model is linear though, and more reliable non-linear dynamics may be necessary to decide whether the upwelling is relevant to the real ocean or not. Analyzing the results from the Community Modeling Effort, Böning et al. (1995) considered the Veronis effect as primarily responsible for the insufficient meridional overturning rate and northward heat transport in their modeled Atlantic. In this respect, the efficient reduction of the upwelling is the most appealing achievement of the frictional closure for tangential velocity within a no-normal-flow boundary condition framework. Nevertheless, oceanic observations and evaluations of this crucial parameter are unfortunately lacking, such that we cannot promote one parameterization over another until better observations of upwelling intensity are made in WBCs.
Seidov (1996) introduced a parameterization of lateral boundary layer in the MOM allowing realistic viscosity coefficients and showed that its influence on the thermohaline circulation was not as important as the one we observe here. Non-linear dynamics plays a significant role in the dissipation of jets normal to coasts and a proper parameterization should include the effect of the full baroclinic instability cascade (Csanady, 1989).
We have compared different parameterizations for momentum dissipation and lateral boundary layers within the same planetary geostrophic mainframe model used at coarse resolution, with identical tracer advection, diffusion, convection and forcing. The Reynolds stress parameterizations we implemented are the traditional Laplacian and the higher-order biharmonic viscosity, the first-order linear Rayleigh friction (in two and three dimensions) and no momentum dissipation at all. The associated boundary conditions are either no-slip, free-slip or various frictional closures for the velocities tangential to the boundaries within a no-normal-flow framework.
The steady-state temperature fields and dynamics after 3000 years of integration allowed a straightforward classification of the models. The PGL group (Laplacian friction), typical of the Modular Ocean Model (GFDL) at coarse resolution, encompasses no-slip and free-slip boundary conditions with either Laplacian, biharmonic or Rayleigh friction. These models are characterized by large vertical (diapycnal) velocities O(10-5 m s-1) along the lateral boundaries (especially upwelling in the WBC and downwelling in the north-east corner), strong WBC and overturning transports. The other group includes three models with horizontal Rayleigh friction and no-normal-flow boundary conditions: frictional closures for the along-shore velocities are derived either from a vorticity equation (Winton, 1993; Winton and Sarachik, 1993), from the relaxation of the hydrostatic approximation with linear friction in the vertical (Salmon, 1986, 1990) or from the addition of biharmonic tracer diffusion (Samelson and Vallis, 1997a, b). By allowing horizontal recirculation of jets impinging on coasts, they achieve a significant reduction of the diapycnal vertical transports along the boundaries (by a factor of 3 to 10), yielding a more efficient thermohaline circulation: cooler deep waters, sharper thermocline, higher poleward heat transport in spite of weaker meridional overturning and WBC transport. In fact, we found that the meridional overturning is a poor indicator of the efficiency of the thermohaline circulation to transport heat poleward. Rather the deep water temperature is well correlated to the upwelling along the western boundary and controls the poleward transport of heat.
The effect of the large upwelling along the western boundary, usually related to the Veronis effect, is two-fold: it provides a shortcut for the thermohaline loop, strongly reducing the intensity of the deep WBC as it travels southward, and cools the upper layer Gulf Stream. Both effects reduce the poleward transport of heat. Furthermore, large western boundary upwelling is often associated with a large downwelling in the north-east corner that drives to depth surface waters warmer than those formed by deep convection. We observed differences in the deep water characteristics of up to 0.5°C: this is easily comparable to the effect of rotating the mixing tensor along the isopycnals or the influence of tracer mixing coefficients. This confirms recent studies enlightening the short-cut of the thermohaline loop as primarily responsible for the weak North Atlantic poleward heat transport in global models (Böning et al., 1995). However, an important implication from this study is that the western upwelling is governed by the lateral boundary layers dynamics, and not only by the thermodynamic "Veronis" effect (at least for our coarse-resolution models). Our results suggest that the large vertical velocities, arising from the horizontal divergence of the quasi-geostrophic velocities close to the boundaries and the application of no-slip or free-slip boundary conditions, increase the slope of the isotherms and create large cross-isopycnals fluxes through the horizontal diffusion operator. Unfortunately, observational evidence of the amplitude of diapycnal upwelling in the Gulf Stream do not allow us to decide which parameterization is the most relevant to the real ocean. Furthermore, all the parameterizations implemented here have their shortcomings (inaccurate geostrophic and especially Sverdrup balance in the interior, or intense diapycnal transports along the boundaries). Therefore we believe that the correct representation of upwelling in WBCs, which is of utmost importance for climate models, will come from a better dynamical understanding of the eddy dissipation in WBCs. Given the influence lateral boundary layers have on the global mass and heat transport, we think that physically-based parameterizations are essential for accurate coarse-resolution ocean modeling.
The parameterization of oceanic lateral boundary layers is an important and overlooked aspect of coarse-resolution climate modeling studies, far more influential than the parameterization of Reynolds stress. It is comparable to the tracer mixing parameterization in its global effects. A proper parameterization based on observations and rationalization of the real ocean physics near lateral boundaries (baroclinic instability cascade, non-linear effects) is required to improve the results of our coarse-resolution OGCMs.
Acknowledgments
. This research was funded through a scholarship awarded to TH from the French Ministry of Research and Space and operating and strategic grants awarded to AJW from NSERC, AES, CICS and the NOAA Scripps-Lamont Consortium on the Ocean’s Role in Climate. We would like to thank A. Fanning for many comments and fruitful discussions about this work, R. Samelson and G. Vallis for providing their scheme and help for its implementation.The different parameterizations for momentum dissipation and lateral boundary layers
We describe the equations and numerical methods used to solve for the different parameterizations of momentum dissipation and lateral boundary layers in the planetary geostrophic models, starting with the models most similar to the MOM and proceeding to the most dissimilar.
PGL (Planetary Geostrophic model with Laplacian friction) is based on the same equations as Colin de Verdière (1988, 1989), but written on a B-grid and employing the iterative method for solving the horizontal velocities proposed by Winton (1993). From the equation for horizontal momentum, we derive a single complex equation for (u+i v),
![]()
![]() .
.
We solve this 2-dimensional elliptic equation at each model level by Successive Over-Relaxation (SOR) for the interior velocities, the boundary speeds being set to zero in application of the no-slip boundary condition. This is not as computationally efficient as Colin de Verdière’s direct solution in spectral space, but much simpler to implement (it can also easily handle irregular geometry). Furthermore, it permits lower viscosity coefficients without generating numerical noise. Laplacian friction is widely used in numerical modeling since its scale selectivity damps out small-scale perturbations. Similar to molecular viscosity in its stress-formulation of surface forces, its mixing scheme conserves energy in the interior and dissipates it along the boundaries by lateral stress.
PGLA (Planetary Geostrophic model with Laplacian friction on A-grid) is the model used by Colin de Verdière (1988, 1989). All the variables (u, v, w, T) are computed on a horizontal A-grid and the horizontal velocities are computed by direct inversion of the tridiagonal matrix resulting from the fast Fourier transform of the spatial fields. No-slip boundary conditions are used, such that only the horizontal grid for horizontal velocities differs from the previous model PGL. The scaling of the Munk boundary layer is straightforward from the vorticity equation: ![]() . Such a scaling leads to a dissipation length scale of (AH/b)1/3. We follow Colin de Verdière’s criterion to determine the viscosity coefficient as a function of the resolution Dx: AH=[1.6-2]¥bĂx3=1.5¥105 m2 s-1 for Ăx=160 km and b at 40°N, which gives a horizontal Ekman number E=AH/(f Dx2) of 0.06.
. Such a scaling leads to a dissipation length scale of (AH/b)1/3. We follow Colin de Verdière’s criterion to determine the viscosity coefficient as a function of the resolution Dx: AH=[1.6-2]¥bĂx3=1.5¥105 m2 s-1 for Ăx=160 km and b at 40°N, which gives a horizontal Ekman number E=AH/(f Dx2) of 0.06.
PGLslip (Planetary Geostrophic model with Laplacian friction and free-slip boundary condition) uses the same momentum dissipation as PGL, but with free-slip boundary conditions: u·n=0 and d(u·k)/dn=0 on the lateral walls, where n and k are vectors respectively normal and tangential to the boundary. Stewart (1989) suggests that both boundary conditions are equally justified at the resolution we use but points out that the no-slip choice results in no net vorticity and meridional vorticity transport in the WBC. Dynamics are solved by the same method as PGL, with the velocities tangential to the boundary equal to the value at the closest inner point for each SOR iteration.
PGBslip (Planetary Geostrophic model with Biharmonic friction) is inspired by high resolution "eddy-resolving" models, as it uses a biharmonic operator for the horizontal friction, associated with free-slip boundary conditions. It is even more scale-selective than a Laplacian formulation, but is known to generate unfortunate local extrema in the velocity field. The horizontal momentum equations become:
![]() .
.
From the relative vorticity (z=vx-uy) equation: bv-fwz = -A4 (zxxxx+zyyyy), the dissipative boundary layer can be scaled as (A4/b)1/5. Its resolution by our grid-spacing defines an otherwise unphysical friction coefficient: A4>b(2Dx)5=(2¥10-11 m-1 s-1)´ (2´ 160 km)5=1017 m4 s-1. This value produces a too narrow boundary current and is increased to 1019 m4 s-1 for the comparison.
PG0 (Planetary Geostrophic model with no friction) implements the purely geostrophic circulation with no-slip boundary conditions on lateral walls. Therefore, in the interior of the domain, the horizontal velocities u and v are computed respectively as -py/(fr0) and px/(fr0); they are both set to zero on the lateral boundaries. Zhang et al. (1992) point out that this parameterization depends on the grid-spacing and no convergence of the results should be expected when the resolution is refined. This is of course an important discrepancy with the previous models, whose momentum mixing formulation and boundary condition make convergence possible. Formally, this formulation is not "well-posed" mathematically but practically, the introduction of numerical boundary layers due to the imposition of the no-slip condition at the coast leads to realistic solutions. This model is also used in conjunction with a free-slip boundary condition (PG0slip) and a no-normal-flow boundary condition as described further with a non-zero linear friction just next to the boundaries (PG0W).
PGR (Planetary Geostrophic model with Rayleigh friction and "no-slip" boundary conditions) implements linear horizontal friction with zero velocities imposed at the lateral boundaries. The velocity field is then a linear combination of the horizontal derivatives of the baroclinic hydrostatic pressure: ![]() .
.
As in the Zhang et al. (1992) model, the velocities on the boundaries are simply set to zero. From the vorticity equation: ![]() , we get a scaling of the width of the Stommel western boundary layer as eH/b. If we want to properly resolve this boundary layer, our horizontal grid spacing needs to be greater than this typical scale. Conversely, for a given resolution of 160 km, eH needs to be greater than b Dx (~3¥10-6 s-1). Assuming a value of 4.38¥10-6 s-1, the non-dimensional Ekman number eH/f equals 0.05, hence the geostrophic balance holds within a few percent in the whole basin. Like PG0, this model assumes a resolution-dependent closure that lacks the physics to match the boundary conditions. It is also implemented with a free-slip boundary condition (PGRslip).
, we get a scaling of the width of the Stommel western boundary layer as eH/b. If we want to properly resolve this boundary layer, our horizontal grid spacing needs to be greater than this typical scale. Conversely, for a given resolution of 160 km, eH needs to be greater than b Dx (~3¥10-6 s-1). Assuming a value of 4.38¥10-6 s-1, the non-dimensional Ekman number eH/f equals 0.05, hence the geostrophic balance holds within a few percent in the whole basin. Like PG0, this model assumes a resolution-dependent closure that lacks the physics to match the boundary conditions. It is also implemented with a free-slip boundary condition (PGRslip).
PGRW (Planetary Geostrophic model with Rayleigh friction and Winton’s vorticity closure) uses the same friction as PGR with a no-normal-flow boundary condition. The new unknowns are then the tangential velocities along the lateral walls, which we determine with the method introduced by Winton (1993). For each level, we write the frictional vorticity equations at the center of each grid-box along the boundaries, using the unknown tangential velocities. This provides as many equations as unknown velocities for each level and just requires solving a wrap-around bidiagonal matrix. The vorticity equation is the same as in PGR. Writing these equations for the center of the tracer boxes (since the velocities are defined at the corners) requires an average of velocities and derivatives carried at the corners and sides of each model box, respectively. Note that this formulation requires friction for the well-posedness of the problem since the determinant of the system for boundary velocities cancels if eH=0. Moreover, this formulation is not successful for solving a cross-equatorial basin circulation. This procedure generates large horizontal velocities along the boundaries, but reduces the vertical velocities along the vertical walls compared to the no-slip boundary conditions as shown in the scaling (section 2c). Thus, a flow hitting a lateral wall recirculates horizontally in the boundary current, instead of vertically in an intense downwelling or upwelling when no tangential velocities are permitted. Since the tangential velocities increase when the grid-spacing decreases, realistic results require that the resolution remains coarse.
PGR4 (Planetary Geostrophic model with Rayleigh friction and biharmonic tracer diffusion) uses linear friction as well with a no-normal-flow boundary condition, but the tangential velocities along the boundaries are determined through the addition of a biharmonic operator for the tracer diffusion. For the details of this formulation, the reader is referred to Samelson and Vallis (1997a, b): The biharmonic diffusion coefficient (K4=4.4¥1014 m4 s-1) is chosen according to these references to reduce the diapycnal fluxes by horizontal diffusion in the WBC.
Finally, PGRS (Planetary Geostrophic model with Salmon’s 3-d linear friction) is based on the full linear equations used by Salmon (1986, 1990):
![]() ,
,
![]() .
.
Salmon (1990) and Samelson and Vallis (1997a, b) resolved this system in numerical models with eH=eV. Salmon (1986) worked out a boundary layer analysis where he pointed out the classical Stommel western boundary, of scale (eH/b)=O(250 km) and a non-hydrostatic lateral zone, of scale (eVH/f)=O(200 m). Willing to resolve the latter without refining our coarse resolution, we decided to use a friction coefficient greater in the vertical than in the horizontal: we managed to increase the latter length scale such that it would be partially resolved by our resolution, without perturbing significantly the hydrostatic approximation in the interior of the basin. The reason for the artificial vertical friction is the well-posedness of the system: maintaining hydrostasy as well as horizontal frictional-geostrophy would entirely determine the horizontal baroclinic velocity field, which could never match the no-normal-flow boundary condition from the bottom to the surface of the lateral walls.
An alternative solution is used in the previous model (Samelson and Vallis, 1997a, b) to avoid the resolution of a 3-dimensional problem: retaining the hydrostatic approximation but adding a biharmonic diffusion of temperature to allow zero heat flux across the boundaries. Nevertheless, relaxing the hydrostatic approximation is very costly numerically, as one shifts from a 2-d (per level) to a fully 3-d problem. The elliptic partial differential equation for pressure is derived by writing the velocities as functions of the first order derivatives of pressure and density (from the momentum equations) in the continuity or the vorticity equation:
![]() .
.
The no-normal-flow boundary conditions are given in terms of the normal and right-handed pressure derivatives (respectively noted by the subscripts n and s) from solving the horizontal momentum equations for the horizontal velocities (similar to PGR):
![]() .
.
These are oblique boundary conditions where the tangential derivative is weighted by a much larger coefficient than the normal one, a characteristic that makes the solution even more complicated as it generates large off-diagonal coefficients in the resolution matrix. The idealized geometry allows a simple decomposition of the solution in terms of vertical modes for pressure. The equations derived for each vertical mode and the details of the solution technique can be found in Huck (1997).
The time stepping is a leapfrog scheme for the advection and Euler backward scheme for the diffusion, occasionally mixed by forward Euler time steps (Euler-backward in the MOM) once every 7 to 17 time steps, except in PGLA where a Matsuno time-stepping proved faster, although it requires the evaluation of diffusion and advection terms twice every time-step. The allowable time step depends largely on the momentum dissipation choice and boundary conditions, extending from 1 day with the MOM code or PG0 to 6 days in PGRS or PGRW. The limiting factor is often the CFL criteria for the vertical advection (but for the northward advection in PGRS and PGRW) in the PG models, which has been related to the speed of frictional waves along the boundaries (Colin de Verdière, 1988; Killworth, 1985). The baroclinic instability in PG equations described by Colin de Verdière (1986) does not occur in our experiments, because of the strong surface restoring boundary condition and the horizontal diffusion of tracer and momentum.
Böning, C. W., W. R. Holland, F. O. Bryan, G. Danabasoglu and J. C. McWilliams. 1995. An overlooked problem in model simulations of the thermohaline circulation and heat transport in the Atlantic ocean. J. Climate, 8, 515-523.
Bryan, F. 1987. Parameter sensitivity of primitive equation ocean general circulation models. J. Phys. Oceanogr., 17, 970-985.
Bryan, K. 1962. Measurements of meridional heat transport by ocean currents. J. Geophys. Res., 67, 3403-3414.
Bryan, K. 1969. A numerical method for the study of the circulation of the world ocean. Journal of computational physics, 4, 347-376.
Bryan, K. 1991. Poleward heat transport in the ocean - A review of a hierarchy of models of increasing resolution. Tellus, 43 AB, 104-115.
Chassignet, E. P. and P. R. Gent. 1991. The influence of boundary conditions on midlatitude jet separation in ocean numerical models. J. Phys. Oceanogr., 21, 1290-1299.
Colin de Verdière, A. 1986. On mean flow instabilities within planetary geostrophic equations. J. Phys. Oceanogr., 16, 1981-1984.
Colin de Verdière, A. 1988. Buoyancy driven planetary flows. J. Mar. Res. , 46, 215-265.
Colin de Verdière, A. 1989. On the interaction of wind and buoyancy driven gyres. J. Mar. Res., 47, 595-633.
Colin de Verdière, A. 1992. On the oceanic thermohaline circulation. Modelling the ocean-climate interactions, J. Willebrand and D. L. T. Anderson, Springer-Verlag, Berlin, 151-183.
Cox, M. D. 1987. Isopycnal diffusion in a z-coordinate ocean model. Ocean Modelling, 74, 1-5.
Csanady, G. T. 1989. Energy dissipation and upwelling in a western boundary current. J. Phys. Oceanogr., 19, 462-473.
Danabasoglu, G. and J. C. McWilliams. 1995. Sensitivity of the global ocean circulation to parameterizations of mesoscale tracer transports. J. Climate, 8, 12, 2967-2987.
Danabasoglu, G., J. C. McWilliams and P. R. Gent. 1994. The role of mesoscale tracer transports in the global ocean circulation. Science, 264, 1123-1126.
Duffield, A. 1993. Thermally-driven Gulf Stream. B. Sc. thesis, Flinders University of South Australia.
Gent, P. R. and J. C. McWilliams. 1990. Isopycnal mixing in ocean circulation models. J. Phys. Oceanogr., 20, 150-155.
Gent, P. R., J. Willebrand, T. J. McDougall and J. C. McWilliams. 1995. Parameterizing eddy-induced tracer transports in ocean circulation models. J. Phys. Oceanogr., 25, 463-474.
Gent, P. R. and J. C. McWilliams. 1996. Eliassen-Palm fluxes and the momentum equation in non-eddy-resolving ocean circulation models. J. Phys. Oceanogr., 26, 2539-2546.
Gough, W. A. and W. J. Welch. 1994. Parameter space exploration of an ocean general circulation model using an isopycnal mixing parameterization. J. Mar. Res., 52, 773-796.
Greatbatch, R. J. and K. G. Lamb. 1990. On parameterizing vertical mixing of momentum in non-eddy resolving ocean models. J. Phys. Oceanogr., 20, 1634-1637.
Haney, R. 1971. Surface thermal boundary condition for ocean circulation models. J. Phys. Oceanogr., 1, 241-248.
Hasselmann, K. 1982. An ocean model for climate variability studies. Prog. Oceanogr., 11, 69-92.
Hirst, A. C. and T. J. McDougall. 1996. Deep-water properties and surface buoyancy flux as simulated by a Z-coordinate model including eddy-induced advection. J. Phys. Oceanogr., 26, 1320-1343.
Holland, W. 1971. Ocean tracer distributions - a preliminary numerical experiment. Tellus, 23, 371-392.
Huang, R. X. and J. Yang, 1996. Deep-water upwelling in the frictional western boundary layer. J. Phys. Oceanogr., 26, 2243-2250.
Huck, T. 1997. Modeling the large-scale ocean thermohaline circulation: Analysis of its interdecadal variability. Ph. D. thesis manuscript, Université de Bretagne Occidentale, Brest, France, 300 pp.
Killworth, P. 1985. A two-level wind and buoyancy driven thermocline model. J. Phys. Oceanogr., 15, 1414-1432.
Lazar, A., G. Madec and P. Delecluse. 1999. The deep interior downwelling, the Veronis effect and mesoscale tracer transport parameterization in an OGCM. J. Phys. Oceanogr., in press.
McCartney, M. S. and L. D. Talley. 1982. The subpolar mode water of the North Atlantic ocean. J. Phys. Oceanogr., 12, 1169-1188.
Masuda, A. and K. Uehara. 1992. A reduced-gravity model of the abyssal circulation with Newtonian cooling and horizontal diffusion. Deep-Sea Res., 39, 1453-1479.
Munk, W. H. 1950. On the wind-driven ocean circulation. J. Meteorology, 7, 2, 79-93.
Oort, A. H., S. C. Ashcher, S. Levitus and J. P. Peixóto. 1989. New estimates of the available potential energy in the world ocean. J. Geophys. Res., 94, 3187-3200.
Pacanowski, R., Dixon, K. and A. Rosati. 1991. The GFDL Modular Ocean Model, Users Guide Version 1.0. GFDL Ocean Group Technical Report #2, 46 pp.
Phillips, N. A. 1963. Geostrophic motion. Rev. Geophysics Space Physics, 1, 123-176.
Rahmstorf, S. 1993. A fast and complete convection scheme for ocean models. Ocean Modelling, 101.
Redi, M. 1982. Oceanic isopycnal mixing by coordinate rotation. J. Phys. Oceanogr., 12, 1154-1158.
Rhines, P. B. and W. R. Young. 1982. Homogenization of potential vorticity in planetary gyres. J. Fluid. Mech., 122, 347-367.
Robinson, A. and H. Stommel. 1959. The oceanic thermocline and the associated thermohaline circulation. Tellus, XI, 3, 295-308.
Robitaille, D. Y. and A. J. Weaver. 1995. Validation of sub-grid scale mixing schemes using CFCs in a global ocean model. Geophys. Res. Letters, 22, 2917-2920.
Salmon, R. 1986. A simplified linear ocean circulation theory. J. Mar. Res., 44, 695-711.
Salmon, R. 1990. The thermocline as an "internal boundary layer". J. Mar. Res., 48, 437-469.
Samelson, R. M. and G. K. Vallis. 1997a. A simple friction and diffusion scheme for planetary geostrophic basin models. J. Phys. Oceanogr., 27, 186-194.
Samelson, R. M. and G. K. Vallis. 1997b. Large-scale circulation with small diapycnal diffusion: The two-thermocline limit. J. Mar. Res., 55, 223-275.
Seidov, D. 1996. An intermediate model for large-scale ocean circulation studies. Dyn. Atmos. Oceans, 25, 25-55.
Semtner, A. J. 1986. Finite-difference formulation of a world ocean model. Proceedings of the NATO Advanced Study Institute on Advanced Physical Oceanographic Numerical Modelling, D. Reidel Publishing Co, Dordrecht.
Semtner, A. J. and R. M. Chervin. 1988. A simulation of the global ocean circulation with resolved eddies. J. Geophys. Res., 93, 15,502-522.
Send, U. and J. Marshall. 1995. Integral effects of deep convection. J. Phys. Oceanogr., 25, 855-872.
Stewart, R. W. 1989. The no-slip constraint and ocean models. Atmos.-Ocean, 27, 542-552.
Stommel, H. 1948. The westward intensification of wind-driven ocean currents. Transactions, American Geophysical Union, 29, 2, 202-206.
Stommel, H. and A. B. Arons. 1960. On the abyssal circulation of the world ocean. II: An idealized model of the circulation pattern and amplitude in oceanic basins. Deep-Sea Res., 6, 217-233.
Straub, D. N. 1996. An inconsistency between two classical models of the ocean’s buoyancy driven circulation. Tellus, 48A, 477-481.
Tandon, A. and C. Garrett. 1996. On a recent parameterization of mesoscale eddies. J. Phys. Oceanogr., 26, 406-411.
Veronis, G. 1973. Large scale ocean circulation. Adv. Applied Mechanics, 13, 1-92.
Veronis, G. 1973. Models of world ocean circulation: 1. Wind-driven, two layer. J. Mar. Res., 31, 228-289.
Veronis, G. 1975. The role of models in tracer studies. Numerical models of the ocean circulation, 133-146. Nat. Acad. of Sciences, Washington DC, 14pp.
Verron, J. and E. Blayo. 1996. The no-slip condition and separation of western boundary currents. J. Phys. Oceanogr., 26, 1938-1951.
Weaver, A. J. and M. Eby. 1997. On the numerical implementation of advection schemes for use in conjunction with various mixing parameterizations in the GFDL Ocean Model. J. Phys. Oceanogr., 27, 369-377.
Weaver, A. J. and E. S. Sarachik. 1991. Evidence for decadal variability in an ocean general circulation model: an advective mechanism. Atmos.-Ocean, 29, 197-231.
Welander, P. 1959. An advective model of the ocean thermocline. Tellus, XI, 3, 309-318.
Winton, M. and E. S. Sarachik. 1993. Thermohaline oscillations induced by strong steady salinity forcing of ocean general circulation models. J. Phys. Oceanogr., 23, 1389-1410.
Winton, M. 1993. Numerical investigations of steady and oscillating thermohaline circulations. Ph. D. thesis, University of Washington, 155 pp.
Zhang, S., C. A. Lin and R. J. Greatbatch. 1992. A thermocline model for ocean-climate studies. J. Mar. Res., 50, 99-124.
|
Model |
Horizontal momentum dissipation |
Vertical momentum dissipation |
Lateral boundary conditions |
Horizontal grid |
Number of vertical levels |
References |
|
MOM |
|
Ø |
no-slip |
B |
15 (90) |
Pacanowski et al. 1991 |
|
PGL |
|
Ø |
no-slip |
B |
15 |
|
|
PGLA |
|
Ø |
no-slip |
A |
15 |
Colin de Verdière 1988 |
|
PGLslip |
|
Ø |
free-slip |
B |
15 |
|
|
PGBslip |
|
Ø |
free-slip |
B |
15 |
|
|
PG0 |
Ø |
Ø |
no-slip |
B |
15 |
Zhang et al. 1992 |
|
PG0slip |
Ø |
Ø |
free-slip |
B |
15 |
|
|
PG0W |
Ø |
Ø |
no-normal-flow* |
B |
15 |
|
|
PGR |
|
Ø |
no-slip |
B |
15 |
Zhang et al. 1992 |
|
PGRslip |
|
Ø |
free-slip |
B |
15 |
|
|
PGRW |
|
Ø |
no-normal-flow* |
B |
15 / 90 |
Winton 1993 |
|
PGR4 |
|
Ø |
no-normal-flow‡ |
B |
15 |
Samelson and Vallis 1997ab |
|
PGRS |
|
|
no-normal-flow† |
B |
90 |
Salmon 1986 |
Table 1. Models description and references.
*
tangential velocities determined through solving frictional vorticity equation along the boundaries†
hydrostatic approximation is relaxed by adding vertical linear friction (-eV w)‡
biharmonic diffusion is added to the tracer equation to determine the tangential velocities
|
Boundary condition Viscosity |
no-slip |
free-slip |
no-normal-flow + frictional closure for tangential velocities |
|
none |
PG0 |
PG0slip |
PG0W* |
|
Rayleigh (- |
PGR |
PGRslip |
PGRW*, PGRS†, PGR4‡ |
|
Laplacian ( |
MOM, PGL, PGLA |
PGLslip |
(not implemented) |
|
Biharmonic (- |
(not implemented) |
PGBslip |
(not implemented) |
Table 2. Model summary: momentum dissipation and boundary conditions.
All dynamical boundary conditions imply no mass transport across the boundaries. In addition, no-slip adds the constraint of zero tangential velocities along the lateral boundaries, while free-slip requires the normal derivative of tangential velocities to vanish along the boundary (no stress); no-normal-flow allows tangential velocities along the boundaries that need to be determined through an additional equation. Note that MOM, PGL and PGLA refer to our control experiments.
*
tangential velocities determined through solving frictional vorticity equation along the boundaries†
hydrostatic approximation is relaxed by adding vertical linear friction (-eV w)‡
biharmonic diffusion is added to the tracer equation to determine the tangential velocities
|
exp. # |
Model Viscosity [m2 s-1] |
Mean Temp. [°C] |
Bottom Temp. [°C] |
Min. Temp. [°C] |
max. MOSF [Sv] |
max. a PHT [PW] |
max. PHT [PW] |
max. G S [Sv] |
pos. max. [°N] |
min. ZOSF [Sv] |
max. ZOSF [Sv] |
West. Upw. [Sv] |
|
1 |
MOM AV=10-3 |
4.228 |
3.531 |
3.461 |
15.42 |
.2204 |
.2308 |
15.0 |
42 |
-4.08 |
7.62 |
5.06 |
|
2 |
MOM AV=0 |
4.230 |
3.533 |
3.464 |
15.39 |
.2204 |
.2308 |
15.0 |
43 |
-4.04 |
7.87 |
5.05 |
|
3 |
PGL |
4.237 |
3.539 |
3.470 |
15.45 |
.2219 |
.2321 |
15.3 |
42 |
-3.84 |
7.99 |
5.14 |
|
4 |
PGLA |
4.251 |
3.547 |
3.478 |
15.47 |
.2203 |
.2304 |
14.9 |
43 |
-3.68 |
8.12 |
5.84 |
|
5 |
PGLslip |
4.189 |
3.477 |
3.405 |
11.14 |
.2258 |
.2360 |
16.0 |
38 |
-3.74 |
8.64 |
4.90 |
|
6 |
PGBslip |
4.238 |
3.509 |
3.434 |
10.70 |
.2235 |
.2341 |
15.0 |
40 |
-3.54 |
9.38 |
5.87 |
|
7 |
PG0 |
4.530 |
3.748 |
3.653 |
15.57 |
.2133 |
.2248 |
19.2 |
33 |
-2.60 |
12.10 |
12.30 |
|
8 |
PG0slip |
4.262 |
3.529 |
3.449 |
10.91 |
.2238 |
.2346 |
16.6 |
34 |
-3.56 |
9.67 |
6.30 |
|
9 |
PG0W |
4.127 |
3.413 |
3.388 |
7.57 |
.2477 |
.2602 |
14.3 |
30 |
-2.03 |
3.70 |
2.95 |
|
10 |
PGR |
4.171 |
3.513 |
3.441 |
14.25 |
.2142 |
.2236 |
11.8 |
42 |
-3.46 |
6.89 |
4.75 |
|
11 |
PGRslip |
4.112 |
3.458 |
3.402 |
12.49 |
.2175 |
.2268 |
12.0 |
42 |
-3.07 |
7.12 |
3.78 |
|
12 |
PGRW |
4.056 |
3.404 |
3.389 |
9.00 |
.2374 |
.2471 |
10.5 |
40 |
-2.30 |
2.79 |
1.94 |
|
13 |
PGR4 |
4.200 |
3.602 |
3.586 |
7.98 |
.2287 |
.2389 |
9.7 |
37 |
-0.44 |
2.14 |
0.63 |
|
14 |
PGRW 90 levels |
4.083 |
3.416 |
3.401 |
9.09 |
.2378 |
.2489 |
10.4 |
40 |
-2.21 |
2.85 |
1.93 |
|
15 |
PGRS e v’=0.03 |
4.080 |
3.406 |
3.392 |
8.71 |
.2375 |
.2486 |
10.3 |
39 |
-1.99 |
2.75 |
1.77 |
|
16 |
PGRS e v’=0.3 |
4.061 |
3.346 |
3.329 |
7.63 |
.2330 |
.2442 |
9.5 |
38 |
-1.36 |
2.45 |
1.46 |
Table 3. Steady-state diagnostics for the different numerical experiments.
Rows 1 and 2 show the small influence of the vertical viscosity in the MOM, given the large horizontal viscosity used. Rows 2 to 16 implement Rahmstorf’s full convection scheme and no vertical viscosity. Column 1 is the experiment number, while column 2 is the model name. Column 3 is the mean basin temperature; column 4 is the bottom temperature averaged from 3950 to 4500 m; column 5 is the minimum temperature achieved at the surface and extending to the lower levels by deep convection. Column 6 is the maximum meridional overturning. Column 8 (7) is the maximum (advective) poleward heat transport. Column 9 is the maximum thermally-driven Gulf Stream transport, whose the latitude is given in column 10. Columns 11 and 12 are the minimum and maximum of the zonal overturning streamfunction. Column 13 is the maximum over depth of the vertical transport in the one-grid-box wide region extending along the whole western boundary (a measure of the Veronis effect).
|
Model |
KE A-grid [J m-2] |
KE B-grid [J m-2] |
APE Oort [105 J m-2] |
APE Ref. [105 J m-2] |
D PE Vert.Mixing [10-3 W m-2] |
- DPEConvection [10-3 W m-2] |
- DPE Dissipation[10-3 W m-2] |
Residual SHF [W m-2] |
Q=Heat Input [W m-2] |
Efficiency=Dissip/Q [10-5] |
|
MOM AV=0 |
104 |
117 |
8.75 |
3.51 |
1.99 |
1.33 |
0.66 |
4.84 ¥10-5 |
12.57 |
5.25 |
|
PGL |
110 |
124 |
7.96 |
3.47 |
1.99 |
1.34 |
0.65 |
1.70 ¥10-5 |
12.62 |
5.16 |
|
PGLA |
112 |
99 |
7.94 |
3.51 |
2.00 |
1.37 |
0.63 |
1.20 ¥10-5 |
12.48 |
5.05 |
|
PGLslip |
144 |
150 |
5.59 |
3.13 |
2.00 |
1.35 |
0.65 |
3.69 ¥10-5 |
13.16 |
4.93 |
|
PGBslip |
187 |
212 |
8.15 |
3.21 |
1.96 |
1.39 |
0.56 |
5.70 ¥10-3 |
12.94 |
4.33 |
|
PG0 |
212 |
436 |
13.00 |
4.23 |
1.91 |
1.91 |
0.00 |
1.98 ¥10-6 |
11.89 |
0.00 |
|
PG0slip |
203 |
258 |
9.35 |
3.28 |
1.95 |
1.43 |
0.53 |
1.85 ¥10-5 |
12.89 |
4.12 |
|
PG0W |
217 |
312 |
2.26 |
1.96 |
2.02 |
0.72 |
1.30 |
4.55 ¥10-4 |
14.70 |
8.83 |
|
PGR |
73 |
87 |
7.82 |
3.28 |
2.00 |
1.23 |
0.77 (0.76 ) |
2.10 ¥10-5 |
11.36 |
6.78 |
|
PGRslip |
82 |
85 |
6.11 |
2.94 |
1.97 |
1.14 |
0.83 (0.75) |
4.47 ¥10-5 |
11.67 |
7.10 |
|
PGRW |
108 |
162 |
2.02 |
1.72 |
2.02 |
0.64 |
1.38 (1.42) |
3.81 ¥10-4 |
13.17 |
10.50 |
|
PGR4 |
116 |
134 |
2.076 |
1.80 |
1.94 |
0.82 |
1.12 (1.17) |
2.00 ¥10-3 |
13.80 |
8.12 |
|
PGRS e v’=0.03 |
104 |
151 |
2.008 |
1.91 |
1.98 |
0.65 (0.07) |
1.33 (1.32) |
3.13 ¥10-4 |
13.17 |
10.10 |
|
PGRS e v’=0.3 |
96 |
131 |
2.014 |
1.99 |
1.99 |
0.68 (0.23) |
1.32 (1.15) |
5.15 ¥10-4 |
12.89 |
10.24 |
Table 4. Energy balance for different steady-states.
Column 1 is the model name. Columns 2 and 3 give the kinetic energy computed on an A and B grid. Columns 4 and 5 give estimations of the available potential energy using the Oort formula or via the method given in section 4a. Columns 6, 7 and 8 show the various contributions to the potential energy balance: the vertical mixing source term and the convective and dissipative sinks. The numbers in parenthesis refer to the estimation of vertical and horizontal linear dissipation of kinetic energy computed as 2
eV KEVertical and 2 eH KE. The residual mean surface heat flux is given in column 9. Column 10 is the heat input, while column 11 gives the thermodynamic efficiency as the ratio of the work produced (rate of production or dissipation of KE) over the heat input Q. Computational details are given in section 4.Figure 1. Mean temperature [°C] and horizontal velocities in the upper 850 m (thermocline) for (a) PGRW, (b) PGL and (c) PG0. The scale for velocities is 1 cm s-1 per degree. Note the western boundary current overshoot, characteristic of the Laplacian viscosity.
Figure 2. Vertical transports [Sv] at the base of the thermocline (850 m) and regions of convection below 250 (dash-dotted line) and 850 m (dashed line) for (a) PGRW, (b) PGL and (c) PG0. Solid contours are for vertical velocities (-10-5, 0 and 10-5 m s-1). The downwelling regions are shaded and the appropriate vertical transports are then downward. Note the large and irregular transports along the boundaries in PGL and PG0 compared to PGRW.
Figure 3. Accuracy of (a) geostrophic and (b) Sverdrup balance for various models. Percentage of the volume of the basin (ordinate) satisfying the balance within a given relative tolerance
e (abscissa):![]() .
.
Figure 4. Meridional overturning streamfunction [Sv; 1 Sv
║106 m3 s—1] and maximum depth of convection (dashed line) for (a) PGRW, (b) PGL and (c) PG0. Note the large variation in the maximum intensity and its position, as well as the more localized convection regions in PGRW.Figure 5. Zonal overturning streamfunction [Sv], meridionally-averaged isotherms (dashed lines) and maximum convection depth over latitude (shaded area) for (a) PGRW, (b) PGL and (c) PG0. Note the slope of the isotherms in the western boundary current for PGL and the narrow region of deep convection in PGRW.
Figure 6. Vertical velocities [10-5 m s-1] along the boundaries, clockwise from the south-west corner to the north-west, north-east, south-east and back to south-west, for PGL, PGRW and PG0.
Figure 7. Zonally-averaged temperature in the thermocline [°C] and maximum depth of convection (dashed line) for (a) PGRW, (b) PGL and (c) PG0. The thermocline becomes more diffuse, mainly because of the warmer deep water temperatures.
Figure 8. Cross correlations of the diagnostics for the 16 experiments in Table 3. Maximum advective poleward heat transport [PW
║1015 W] as a function of (a) meridional overturning and (b) mean bottom temperature. (c) Meridional overturning and (d) western upwelling as a function of mean bottom temperature. r is the correlation coefficient (the 95% confidence level for the 16 models used is 0.48) and the solid line is the linear regression solution.
Figure 9. (a) Minimum, mean bottom and mean basin temperature [°C] for PGL (solid lines) and PGRW (dashed lines) as a function of horizontal tracer diffusivity in a log-log plot. For each model, the upper curve is the mean basin temperature, the middle one is the mean bottom temperature (at 4225 m deep) and the lower curve is the minimum temperature, usually achieved from the surface to the bottom through convection. Note the shift between the 2 lowest curves for PGL compared to PGRW (related to the variability in the deep water temperatures) and the inversion at low diffusivity due to numerical problems (high Peclet number). (b) Maximum over depth of the upwelling integrated along the western boundary (x) and meridional overturning for PGL (solid) and PGRW (dashed). Note the positive correlation between the 2 in PGL (0.68) but negative in PGRW (-0.91).
On the influence of the parameterization of lateral boundary layers
on the thermohaline circulation in coarse-resolution ocean models
T
HIERRY HUCK, ANDREW J. WEAVER AND ALAIN COLIN DE VERDIÈREABSTRACT
*1. Introduction
*2. The models
*a. The planetary geostrophic dynamics
*b. Various parameterizations for Reynolds stress and lateral boundary layers
*c. A scaling for the vertical velocities in various lateral boundary layers
*d. Model geometry, parameters and forcing
*e. Preliminary grouping of the models and their results
*3. The Veronis effect and the efficiency of the thermohaline circulation
*a. The mean circulation
*b. The geostrophic and Sverdrup balances
*c. Vertical velocities and overturnings
*d. The mean stratification
*e. Poleward heat transport
*f. The thermohaline efficiency
*4. Energetics
*a. The potential energy balance
*b. Comparison of the energy balance for the different models
*c. A thermodynamic thermohaline efficiency
*5. Discussion
*a. The Veronis effect revisited
*b. Sensitivity to horizontal or isopycnal diffusion
*c. Relevance of the large upwelling in the western boundary current
*6. Conclusion
*APPENDIX: The different parameterizations for momentum dissipation and lateral boundary layers
*REFERENCES
*Table 1. Model description and references.
*Table 2. Model summary: momentum dissipation and boundary conditions.
*Table 3. Steady-state diagnostics for the different numerical experiments.
*Table 4. Energy balance for different steady-states.
*Figure captions
*