Submitted to:

Journal of Climate

February 4, 1999

A. Colin de Verdière

Laboratoire de Physique des Océans

Université de Bretagne Occidentale

6 avenue Le Gorgeu, B. P. 809

29285 Brest cedex, France

email: acolindv@univ-brest.fr

A four box model of the ocean — atmosphere is constructed that exhibit self sustained oscillations in the regime of decadal to interdecadal periods found in oceanic general circulation models under certain boundary conditions. The oscillations are assumed to be caused by a type of baroclinic instability that relies on the store of available potential energy in the ocean. To represent this process in a low order model, we propose Landau’s equation to govern the evolution of the overturning branch of the oceanic circulation. The domains of the unstable oscillations are found from linear stability analyses and the non-linear regimes are explored numerically. On these long time scales the atmospheric temperatures follow the oceanic temperatures. If the atmospheric temperatures are forced to be constant, the oscillations become strongly damped and disappear. The implications of the simple physics of this model to the decadal oscillations observed in more complex two- or three-dimensional GCMs are discussed.

The North Atlantic oscillation (NAO) is the best example of the existence of climate variability on the decadal time scale (Hurrell and Van Loon 1997). The good correlation between the strength of the westerlies and the large scale SST anomalies in the North Atlantic shows that both the atmosphere and ocean are active in the oscillations and the basic question, unanswered so far, is whether the NAO is an internal mode of the atmosphere with the ocean reacting passively, the converse or neither i.e. intrinsically coupled modes. Because decadal time scales are in the range of periods of free oceanic waves (baroclinic Rossby waves suitably modified to take into account the existence of an underlying mean circulation), it is highly likely that the ocean plays a central role. Over the last ten years, numerous simulations of the large scale ocean circulation (Cai et al. 1995; Capotondi and Holland 1997; Greatbatch and Peterson 1996; Greatbatch and Zhang 1995; Huang and Chou 1994; Weaver and Sarachik 1991; Weaver et al. 1993; Huck et al. 1998; Winton 1996) under boundary conditions of given flux at the air-sea interface for at least one of the temperature or salinity variable show unequivocally that decadal oscillations are generic features of the oceanic model response. As the diffusion or surface flux sensitivity to SST are sufficiently lowered (Chen and Ghil 1996; Colin de Verdière and Huck 1998–CVH in what follows), they appear spontaneously in the form of large-scale surface intensified thermal anomalies of a few degrees. They are more intensified in the Northern part of basins and are associated with fluctuations in the western boundary current transport and global overturning of a few Sverdrups. It has been suggested by CVH that the cause of these oscillations is the baroclinic instability of the mean state in the region of strongest surface heat losses. When the oscillations are nearly monochromatic, two variables are necessary to the existence of the oscillatory states. We need then to derive model equations for these two variables that may reproduce the physics present in models of higher complexity. Stommel (1961) pioneered this approach to show that a two-box ocean model with overturning proportional to density differences between the boxes could exhibit multiple steady states provided that temperature and salinity were restored to surface values with different time constants. This suggestion of the existence of multiple states in OGCM and box models of increased complexities was explored by Bryan (1986), Marotzke (1990), Weaver et al. (1993), Marotzke and Willebrand (1991) and many others in the context of mixed boundary conditions i.e. restoring on temperature, and flux on salinity. Decadal oscillations were first observed in such simulations by Weaver and Sarachik (1991) who suggested an advective mechanism. However a fluid with two components of state is not necessary as fixed flux experiments with either salinity (Huang and Chou 1994), or temperature alone (Greatbatch and Peterson 1996; Greatbatch and Zhang 1995; Huck et al. 1998) demonstrated later. Many authors used 2D OGCMs and none reported decadal oscillations (see Winton 1996) until recently Drbohlav and Jin (1998) reported some. Prior to this last study, the dynamics used in these models were roughly speaking similar to that used by Stommel with friction (acting on meridional velocity) balancing the meridional pressure gradient with ad hoc coefficients supposed to mimic some effects of the rotation. Realizing that the meridional circulation is not in equilibrium with the density field in the decadal oscillations observed in 3D models, Drbohlav and Jin turned to unsteady dynamics and let meridional accelerations respond to meridional pressure gradients. We will point out that the long period oscillations that they obtain have very different physics from what happens in three dimensions.

Ruddick and Zhang (1996) revisited Stommel’s box model, and added some new features such as a non linear dependence of the overturning with density contrast and a temperature dependent hydrological cycle but concluded that the model was unable to oscillate. Griffies and Tziperman (1995) proposed another box ocean model adding a separation between thermocline and abyssal waters to Stommel’s original formulation. They showed the existence of a damped oscillatory mode about a thermally dominant state and proposed the idea that white noise atmospheric forcing of such a mode could be responsible for the variability found in the coupled climate model of Delworth et al. (1993). Even more ambitious box models have been put forward by Birchfield (1989) coupling an energy balance model of the atmosphere to a three box ocean with active temperature and salinity components. He recovered Stommel’s thermally and salinity dominant states and discovered the existence of amplified century long oscillations when the evaporation was sufficiently strong. This oscillatory state was transient as the system showed abrupt bifurcations to the salinity dominant steady state. Welander was very inventive in the construction of simple fluid oscillators. He proposed one in 1982 made of a surface box that relaxed box values of T and S with surface values on different time scales and mixed to a large reservoir whenever surface density exceeded the density of the reservoir. This convective oscillator needs two components to work and so cannot be directly relevant to the physics of one variable decadal oscillations. To summarize what has been done so far, it seems therefore that there is a need for a box model that would allow self sustained oscillations in the regime of interdecadal periods and that do not require a two component oceanic fluid (with different boundary conditions for temperature and salinity) since OGCMs oscillate with a single component fluid. Given the general complexity of GCMs, it is necessary to test ideas with simpler analogs that have a limited number of freedom and allow to go up and down the scale of complexity with added focus on specific processes, whose physical understanding are prerequisites for climate predictability studies. Steps in this direction for decadal oscillations were made by CVH who suggested from a study of the linear perturbations of a four box ocean-atmosphere model with heat exchanges only, that the perturbations could indeed oscillate provided first the existence of a phase lag between the overturning and the equator to pole temperature contrast and second an instability process sufficiently active to overcome the stabilizing effect of the diffusion. The above phase lag is indeed an observed feature in OGCMs simulations (Greatbatch and Peterson 1996; Huck et al. 1998) and a number of supporting elements for the presence of an active baroclinic instability in OGCMs simulations were brought forward by CVH. There was however a major hypothesis in their perturbations equations that amounted to neglect the advection of temperature anomalies by the mean flow. Although this damping term was shown to be small in Huck et al. (1998) analysis of OGCMs simulations, the model could not be considered a complete physical analog of the OGCMs oscillations. The objective of the present study is to reject CVH’s hypothesis and bring an answer to this problem. We propose a two-degree of freedom dynamical system that oscillates on decadal periods and ultimately rest on plausible physical grounds. The evolution of temperature contrast obeys a heat transport equation identical with Stommel’s (1961) formulation but the equations for the overturning is different: its rate of change is made proportional to the product of the overturning itself and a measure of the available potential energy in the ocean. A frictional term is added to stabilize the system at large amplitudes. This choice is derived after an analysis in Section 1 that demonstrates that the laws governing the overturning are severely limited if self sustained oscillations are to exist with the constraints of the heat transport. Assume for instance that somehow the overturning is less than at steady state, then the surface heat fluxes are going to build up the equator to pole temperature contrast and if the overturning respond immediately to this build-up then the increase in advective heat transport reduces the temperature contrast and the system returns to its original position, the basis for the non-oscillation of Stommel’s model as studied by Ruddick and Zhang (1996). The solutions of the proposed box model are analyzed in Section 2 and 3: the stability analysis of the fixed points is performed and the properties of the oscillations in the non-linear regimes are found numerically. Some implications of these results for the decadal oscillations found in OGCMs are discussed in section 4. A detailed comparison with the results of a three dimensional ocean model coupled to a one layer energy balance model of the atmosphere shows encouraging support for the box model parameterization. However the non-linear regimes shows some significant differences. The last part offers a discussion in the light of recent results that have appeared in the literature. In particular we show that Drbohlav and Jin’s (1998) two-dimensional oscillations have very special physics that do not qualify as good analogs of oceanic oscillations.

Consider the situation in figure 1 where two atmospheric boxes are coupled to two oceanic boxes. The atmospheric boxes exchange heat externally through incident solar flux Q_S and infrared back radiation flux Q_L to outer space. We assume that the heat flux Q_A0 between ocean and atmosphere is simply equal to l (T_A — T₀), the difference between atmospheric and oceanic temperatures. Because the characteristic time scale of response of the atmosphere to an oceanic temperature anomaly which is in the range of days to weeks is small compared to decadal time scales, it is an excellent assumption to assume that the atmosphere is in energy balance with the fluxes adding to zero:

(1)

where the indices i = 1, 2 (j = 3-i) refer to the tropical and polar atmospheric box respectively and K_A is the turbulent eddy heat conductivity that parameterizes lateral eddy transport. For the range of temperature variations of interest, the Stefan-Boltzmann’s law can be linearized (Budyko 1969) so that:

Q_L = A + B T_A

Making this substitution in (1) gives an equation for y = , the temperature difference between the two atmospheric boxes, in term of the temperature difference between the two oceanic boxes:

D Q_S — By - l (y — x) — 2 K_Ay = 0 (2)

where D Q_S = is the net differential solar input at the top of the atmosphere. Dependence on absolute temperature drops out in (2) because we have assumed for simplicity the same coefficients A and B for each box for the linearized expression of the infrared flux. This symmetry condition allows to derive expressions that depend only on the temperature differential between the boxes and not on the mean temperature of the boxes. We are only concerned here with internal redistributions in the ocean — atmosphere system.

Both y and Q_A0 the flux driving the oceanic boxes can then be expressed in terms of x:

(3)

and (4)

Atmospheric temperature anomalies follow closely (and linearly) oceanic temperature anomalies with a "slope" l /(l + B + 2K_A) of 0.77 when values of l = 15 W m^-2 °K^-1, B = 1.7 W m^-2 °K^-1, K_A = 1.3 W m^-2 °K^-1 are inserted. The values of B and K_A are those chosen by Marotzke and Stone (1995) in their study of the sensitivity of climate models to flux corrections. The value of l corresponds to those of Seager et al. (1995): It is well below the threshold found in OGCMs (CVH) beyond which no decadal oscillations exist. The ocean-atmosphere heat flux is dominated by the differential of solar flux, the first term on the RHS of (4) for all reasonable values of oceanic temperature differences. This occurs because the box model captures only the largest scales of spatial variability much larger than the atmospheric diffusive length scale of the order of 700 km, discussed by Marotzke and Pierce (1997). Equation (4) solves the energy balance of the atmospheric box model by providing the surface flux in terms of oceanic temperatures only.

Turning our attention to the oceanic compartment, two processes are included to transport heat meridionally, turbulent eddies akin to those included in the atmospheric compartment but more importantly the large scale thermohaline circulation made possible in the ocean by the existence of meridional boundaries. The term "thermohaline" is improper in our context since fresh water and salt transports are not considered in this study but we will stick nevertheless to this usual convention.

The heat conservation equation for each oceanic box is:

(5)

with h and A (5000 km ´ 2000 km) are respectively the depth and area of each box, y is the overturning stream function (m³ s^-1) and K₀ the eddy heat conductivity (in W m^-2 °K^-1). Because decadal oscillations appear as surface intensified phenomena in OGCMs, the subtropical box will be taken to have a depth h of 1000 m, much less than the depth of the ocean. The polar box with active convection should have a much greater depth and connect to deep abyssal boxes as in Huck et al. (1998). However if we want to preserve symmetry conditions that allow to focus on temperature differentials only, we need to have a polar box identical with the subtropical one. Including explicitly a deep abyssal layer would allow to predict mean temperatures as well. However the adjustment time scale of the deep ocean is at least one order of magnitude larger than decadal time scales and these processes are purposely filtered out. After introducing a time scale t (= 1 year) for the time variable, and a scale hA/t for y , (5) can be transformed into an equation for the oceanic temperature difference x between the tropical and polar box:

= a l (y — x) — 2 y x - 2a K_Ox (6)

where a = is a constant (in K m² W^-1). The variable y can now be eliminated between (4) and (6) to yield a single equation for x:

= q - 2y x - d x (7)

where q, the driving flux is and d the diffusion is: summarizing the cumulative effects of eddy heat transports in the ocean and in the atmosphere and infrared back radiation. Lagrangian marker dispersal in the ocean gives eddy diffusivity estimates in the range of 10³ m² s^-1 that translates to eddy heat conductivities of 10³ ´ (r C_p h)₀/L² where the appropriate length scale L over which the diffusion process is analyzed, is made equal to the meridional size of the box. Values for h (L) of 1 km (2000 km) respectively, give K₀ ~ 1 W m^-2 °K^-1. It is readily seen that the three contributors to the diffusion in (7) have the same order of magnitude, giving an overall diffusion time scale d ^-1 of 23.7 y. The remaining contributor to the heat transport which is needed to respond to the differential flux q in the steady state comes from the overturning that adjusts a surface temperature anomaly on a time scale (2y )^-1 ~ 10 y under typical "present day" conditions of 15 Sv for the equator to pole mass transport. This is twice as efficient as the sum of turbulent diffusion and infrared losses.

A dynamical equation must be added to the heat advection-diffusion equation (7), to give the relation between the time rate of change of the overturning and temperature. There are additional effects linked with variations of the eddy diffusivities K_A and K_O with temperature gradients but we have decided to concentrate solely upon the overturning. OGCMs readily provide the overturning streamfunction in the latitude — depth plane, the quantity being determined by the zonal pressure gradient a quantity that does not lend itself to easy parameterization in zonally averaged or box models. Originating with Stommel (1961), numerous studies have appeared that ultimately rest upon a steady state balance between the buoyancy torque proportional to x and dissipation proportional to y with no phase lags. The absence of phase lags may well be justified for very long time scales much larger than the decadal scales baroclinic signals but clearly inappropriate here, as shown by Greatbatch and Peterson (1996) and CVH. These studies have shown the existence of quadratures that must be included in lower order models that aim at reproducing the behavior of GCMs. Ruddick and Zhang (1996) recently added support to this requirement by proving the non-oscillatory nature of the original Stommel, 1961’s box model. A generic form of our dynamical predictive equation for y is therefore:

= f(x,y )

The problem is now to discover the functional dependence f(x,y ) that reproduces unstable oscillatory fixed points that appear under Hopf type bifurcations when the diffusion is progressively lowered. The existence of Hopf bifurcations in OGCMs from a steady THC regime to an oscillatory one has been shown by Chen and Ghil (1996) against variations of l and by CVH against variations of eddy diffusivity. The later authors showed that this was made possible, first by an instability process concentrated in the western boundary current extension of their oceanic basin i.e. the regime of baroclinic instability at scales large compared to the Rossby radius of deformation and second by the existence of planetary potential vorticity (PV) modes in the interior. As will be shown next, relatively simple and physically plausible forms for f(x,y ) allow to recover these three-dimensional effects. It is of course illusory to recover the hydrodynamics of oceanic baroclinic instability in one layer, two-box fluid model, but its salient physical effects can be parameterized. We present the results voluntarily in an unusual fashion by showing first how a simple functional dependence for f(x,y ) allows a supercritical Hopf bifurcation of the two degree of freedom dynamical system and later justify the necessarily non-unique form that has been chosen from a physical point of view.

Consider the steady state equation imposed from (7): .

Any point on this curve (figure 2) in the x,y phase space for which f(x,y ) vanishes is a fixed point of the dynamical system. Largest x (= q/d ) is obtained when y is zero. In this diffusive state the heat input is balanced entirely by eddy heat transport and infrared back radiation. A non-zero overturning requires less meridional temperature difference to balance a given surface flux. In the neighborhood of a fixed point of coordinates (x₀,y ₀) arbitrary at this point, the linearized equations for the perturbations are:

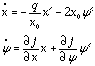
in which the f partial derivatives are evaluated at the fixed point. Exponential solutions el ^t require the exponent l to obey:

The conditions for the fixed point to be a spiral source (l _R > 0, l _i ¹ 0) require:

(8a)

(8b)

Therefore a weak necessary condition for oscillatory instability is that both partial derivatives be positive. This implies in turn that be negative at the fixed point so that the intersection of the heat curve with the dynamic curve of equation f(x,y ) = 0 must occur with a negative slope as sketched in figure 2. This surprising conclusion is opposite to the choices of Stommel’s type parameterizations for which y is an increasing function of x and provides the key to the existence of unstable oscillatory states. There are two other requirements that help to further select a functional form for f. The first is that the diffusive state be a fixed point and for this to be the case f(x,y ) must be of the form y g(x,y ). The second is that friction must be active to equilibrate buoyancy torque for large values of y . The dynamical system must be dissipative i.e. both for diffusive and frictional arguments at large values of x and y . This implies that the curve of equation f(x,y ) = 0 pictured in figure 2 must change slope for large values of y . The simplest continuous curve with a change of sign in slope is a parabola and g is then chosen to be of the form:

g(x,y ) = k(x-x*) - g (y -y *)².

These considerations lead us to consider as a prototype for interdecadal oscillations the system:

= q - 2y x - d x (9a)

= k(x — x*) y - g (y - y *)² y (9b)

where k, g , x* and y * are free parameters. These parameters are severely constrained if we require the existence of only one extra fixed point (in addition to the diffusive state) and furthermore that this extra fixed point be a spiral source. A somewhat unusual path has been used to "find equation 9b" from properties of its solutions. The non-unique choice for f is, of course, highly artificial unless a physical interpretation be given. The first term on the RHS of (9b) tells us that if the north-south temperature contrast exceeds a given bound then that term is responsible for an exponential increase of y . One of the results of the analysis of OGCMs by CVH is that the driving behind the interdecadal oscillations is the baroclinic instability of the western boundary current. In that context, the first term in (9b) mimics the instability that occurs when potential energy is available to be converted in kinetic energy. Since x is a measure of the meridional temperature gradient, the thermal wind associates a vertical shear of a zonal current, so that in agreement with baroclinic instability, the growth rate is made proportional to the vertical shear of that zonal current. The presence of a threshold x* to initiate exponential growth is not essential but is a matter of simplicity. If x* is absent, the parabola cuts the heat curve at a second fixed point. By our previous arguments, that second fixed point (higher y , lower x) is stable since the slope of the parabola is positive there. As we have no particular examples of OGCMs experiments in mind that would justify the presence of this additional stable fixed point, this is not further considered in what follows and we use non-zero x* (and y *) to insure the existence of a single advective fixed point which necessarily occurs at x,(y ) larger (smaller) than x*,(y *). The second term on the RHS of (9b) models turbulent friction by restoring the overturning to y * for large values of y . It ensures dissipation of the dynamical system by saturating the amplitude of the unstable perturbations. Precisely at the fixed point, buoyancy torque balances the friction as in Stommel’s (1961). But we have argued that these terms cannot equilibrate at all times on the time scale of baroclinic planetary waves and re-emphasize that the prognostic nature of equation (9b) is essential. One might object to the formulation of the friction term on the basis that equilibrium solutions of OGCMs tend to have overturning varying linearly with imposed surface temperature contrast. The present formulation with fixed values of x*,y * provides a steady state overturning varying as the square root of the atmospheric temperature contrast in place of the linear law. However it is clearly unphysical to vary the external forcing and keep restoring to the same x*,y * state. The proper variation of overturning against externally imposed temperature contrast must go along with adequate parallel variations of x*,y *. Consequently we can use the model only locally in parameter space to understand the conditions under which decadal oscillations appear around a fixed point for given values of x*,y *. Note that in our coupled case, the only external parameter is the solar flux D Qs and it is not a restriction to keep it constant since our primary hypothesis is to explain decadal oscillations as internal modes of variability of the climate system. One last comment is that (9b) is Landau’s equation, an equation used to describe the transition to turbulence through hydrodynamic instabilities. Landau used that equation in its simplest form to show that at a critical Reynolds number, the system could bifurcate along the road to turbulence from a laminar flow to a time dependent periodic one (see Drazin and Reid 1981 for a review).

We now proceed to examine in detail the properties of the set (9). First of all in order to have a single fixed point (in addition to the diffusive one) in the situation of figure 2 the parabola must intersect the y = 0 axis below the diffusive equilibrium temperature contrast q/d and its minimum must be above the heat curve, requirements for the parameters that translate into:

(10)

These inequalities will be assumed to hold in what follows and under these conditions the two fixed points are:

the diffusive state, while the second "advective" fixed point is solution of the cubic:

(11)

At most one real root is solution of (11) under conditions (10). Instability of the fixed points depends on condition (8a) that becomes:

(12)

This condition can be quickly recovered by forming the divergence of (9).

(13)

At a fixed point 2y + d is just q/x and the condition of a positive divergence gives back (12). The oscillatory nature of the dynamical system depend on whether the divergence takes both signs in the x,y plane, a necessary condition known as the Poincaré-Bendixon theorem. It is immediately fulfilled when the instability condition (12) is met because (13) shows that the divergence becomes negative for large values of y (for a given x), a condition that shows the dissipative nature of the system. The condition for imaginary exponentials (8b) is easily obtained from the linear stability analysis.

In the exploration of parameter space, the values of x*,y * have been fixed with values representative of the THC of the modern ocean. The parameter k bears upon the time scale of the oscillations as can be inferred from (8b). It is linked to the phase lag that does exist in the ocean between the western boundary current transport and the interior temperature gradient lag that depends on the time it takes for a planetary wave to cross the basin (Huck et al. 1998). Only the friction g and the diffusion d are varied in the parameter space exploration that is presented next. Fixed parameter values are: k = 0.1 y^-1 °C^-1, y * = 15 Sv, x* = 11.715 and D Q_S = 100 W m^-2. The oceanic boxes extend 5000 km (2000 km) in longitude (latitude) and are 1000 m deep. The real part of the eigenvalues (i.e. the growth rates) near the diffusive and advective fixed points are shown in figure 3 with respect to g and d . The growth rates of the diffusive solution is positive (negative) for small (large) d . With the value of d previously estimated, the diffusive solution is therefore always unstable almost independently of the value of g . It can also be shown that it is non oscillatory. Since the temperature contrast of the diffusive solution is much larger than x*, positive y perturbations are amplified exponentially through the action of the instability term (first term) on the RHS of (9b). The analysis of the advective solution shows that its stability boundaries are more complex. For each g there are limits in d beyond which (11) has either two roots or no root. Only the domain inside the limits given by (10) has been explored. First g must exceed a certain cut-off value for the fixed point to be unstable for a given d . Conversely for g above this cut-off, the fixed point is stable for sufficiently low and sufficiently high d values. The former result is counter-intuitive. It comes from the fact that as d decreases to low values, y increases and x decreases in a combination that makes the system more dissipative. At the difference of the diffusive case, larger temperature contrast and smaller overturning are now obtained for larger diffusion and friction. In the whole domain of existence of this fixed point, the perturbation solutions are oscillatory. Their frequency depends weakly on g and decreases with increasing diffusion as expected. The divergence (not shown) has exactly the same shape as the growth rate in the d , g space.

It is now possible to turn to the temporal description of particular solutions. With the diffusion d = 4.2´ 10^-2 y^-1 previously estimated, and k (= 0.1 °C^-1 y^-1) typical of the sensitivity observed in OGCMs, figure 4 shows the rms amplitudes of the temperature perturbations at large times as functions of g . It is surprising at first to see the perturbations growing with an increase in the friction parameter g . This comes from the fact that as g increases, the distance of the fixed point y ₀ to y * diminishes. The square of that distance appears in the friction parameterization and this effect overrules the increase in g so that the net friction near the fixed point decreases. For values of g larger than g _c (= 100.5), the fixed point becomes unstable in an oscillatory manner at a value well predicted by the linear analysis (12). The dependence of amplitudes of the limit cycle on (g - g _c)^1/2 is the familiar signature of a supercritical Hopf bifurcation at g _c. Equations (8a) shows that the critical condition at bifurcation gives ¶ f/¶ y equals q/x₀ (= 1.22/12.02) implying an exponential amplification of y in slightly less than 10 years. We recover the kind of efficiency measured by the parameter m in CVH. With parameters inside the instability regions (g = 105) small perturbations grow over a 1000 y time scale to finite rms amplitude of 0.6°C (2 Sv) with oscillations of about 25 y period around the advective fixed point at 12.03°C (9.48 Sv). Note that these realistic amplitudes of the oscillations are obtained for values of g near bifurcation. This implies in turn that the growth rate is very much smaller than the period (23y) by almost two orders of magnitude. This result holds for infinitesimal perturbations at the fixed point. Of course the convergence to the limit cycle can be much more rapid if the system is more strongly perturbed. In particular if the initial state lies outside the orbit of the limit cycle, convergence to the limit cycle occurs on the time scale of the period. The situation is illustrated on the phase portrait in figure 5c for a few trajectories that are initialized on the edges of the domain. When the THC (y ) is large initially, the dynamical system moves rapidly to a state of low THC, that is itself unstable and is attracted very rapidly to the limit cycle. The temperature perturbations in the atmospheric box are always in phase with oceanic temperatures (3), a result that comes from the weak assumption of low thermal inertia of the atmosphere at decadal scales. For the parameters chosen, their amplitudes are about 77 % less than oceanic temperatures. The surface heat flux differential applied to the oceanic box is nearly constant about 57 % of the solar flux differential at the top of the atmospheric box. While OGCMs have been run for a long time with a restoring boundary condition on temperature, more recent computations either with constant surface flux or coupling to Energy Balance Models have revealed the emergence of decadal oscillations. The nearly constant surface flux of this coupled box model that captures but the largest scales of variability shows the relevance of the simple constant flux experiments. To further appreciate that the model is a physical analog of the behavior of OGCMs we have studied the effect of a switch to restoring boundary conditions. We know from (3) the atmospheric temperature contrast y_o that is prevalent at the advective fixed point. When the limit cycle is well established, we suddenly freeze the atmosphere by fixing y to y_o in (6). The oscillations are now observed to be strongly damped and the system converges back to the advective fixed point in less than 100 years. This result that agrees with OGCMs transitions is not difficult to understand. When y is fixed, the heat equation has the same form as (7) but with a new repartition between forcing and diffusion leading to different values of q and d . The damping that comes from the diffusion d increases to a value a (K_o + l ), a factor of 3.2 larger than the diffusion of the free atmosphere case for the values of the chosen parameters. The diffusion of the frozen atmosphere case can be shown to reach the much lower diffusion of the free atmosphere only at the price of reducing the air-sea exchange coefficient l to values small compared to B + 2 K_A.

The rate of growth to finite amplitudes measures the strength of the instability and governs the level of the oscillations at saturation. While the limit cycle in x,y space is nearly elliptical at values of g just above supercritical (figure 5c), it becomes already strongly distorted for higher values of g due to non-linear effects. The oscillation slows down very much when the overturning comes nearly to a stop in the trough of the oscillation. It stays at low values for half a period during which the temperature contrast increases almost linearly in response to the surface flux (since the advection is weak) (figure 6). At a given temperature threshold, the overturning rises brutally, the instability term in (9b) exceeding the frictional term. In the mean time the temperature starts to decrease quickly since the advection works to eliminate the temperature contrast. The instability term in (9b) goes back under the threshold and y starts to decrease but less rapidly to low values. During the long diffusive rise that follows, the instability and frictional terms remain small. It is presumably this effect that causes the period to increase markedly in the non-linear regime (41 years at g = 300), almost twice the value in the linear regime near bifurcation.

The parameterization of the box model provides a simple model for the existence of oscillations that may be useful for conceptual purposes. Its strength, if any, must come from a comparison with three-dimensional models. Some important features such as the transition from steady to oscillatory states through supercritical Hopf bifurcations (Chen and Ghil 1996; CVH) are built in our box model parameterization. If we insist that the important variables that govern the oscillations are the north-south temperature contrast and the overturning stream function, we could estimate these variables in a coupled model simulation and check whether their rates of changes are governed by relationships similar to the box model equations (9). To meet this objective at the lowest possible cost, we set up a three-dimensional ocean model coupled to an atmospheric energy balance model (EBM). The ocean model is described in Huck et al. (1997, 1998): the dynamical part is based on the planetary geostrophic equations with Laplacian horizontal viscosity (A_h=10⁵ m² s^-1) and no-slip boundary conditions but no vertical viscosity (which would be negligible given the large horizontal diffusivity necessary to resolve the Munk boundary layer), no bottom friction nor wind forcing (such that the barotropic mode in a flat-bottom basin is zero); the thermodynamical part is limited to the equation for temperature with a linear equation of state (a =2´ 10^-4 K^-l): advection, diffusion (horizontal and vertical diffusivities are constant, respectively 1000 and 10^-4 m² s^-1), convection (as described by Rahmstorf 1994), and surface forcing.

The equations are discretized on an Arakawa B-grid in Cartesian coordinates, for a mid-latitude b-plane ocean basin centered at 40° N, extending from 20° to 60° N, 5120 km wide and 4500 m deep. The resolution is relatively coarse: 160 km horizontally and 15 levels vertically (respectively 50´ 3, 100, 150, 200, 250, 300, 350, 400, 450, 500, 550´ 3 m thick).

The atmospheric EBM is a one layer atmosphere (heat capacity is 10⁷ J m^-2 K^-l), absorbing incoming short wave from the sun at the rate of 157 W m^{-2 ´} cosinus[p ´ (latitude
-20°)/40°], such that the mean heating (cooling) is 100 W m^-2 in the southern (northern) half of the domain and radiating infrared to space as a linear function of its temperature
(B=1.7 W m^-2 K^-l). The horizontal heat transport is parameterized as a diffusion law with a constant coefficient of 0.5´ 10⁶ m² s^-1. The horizontal grid is identical to the ocean's, while the Euler integration requires a much shorter time step (1 hour). The exchange of heat between the atmosphere and the ocean is proportional to the difference between the atmospheric and oceanic surface temperature (exchange coefficient of 15 W m^-2 K^-l). Geometry, parameterizations and parameters were chosen to be as similar as possible to the box model. The coupled integration spans 6000 years, the time for the oscillations amplitude to settle. The mean overturning is then 10 Sv, with a standard deviation of 0.5 Sv. Meanwhile, the temperature difference between the upper 850 m southern and northern half ocean boxes varies by 0.1°C around 3.7°C. The oscillation period is then very close to 20 years. Within such a small amplitude regime, the oscillations are very smooth and regular (figure 7) but not perfectly sinusoidal though: the meridional overturning rises very linearly on a 14 year time scale but drops sharply within 5 years. Although not as asymmetric, the temperature difference between the upper boxes starts rising 3 years before the overturning, peaks 5 years after it started, and declines more smoothly for the remaining 12 years. These asymmetries are stronger when the amplitudes are larger in the early part of the coupled run. This behavior must be contrasted with the box model results in the non-linear case that are clearly different (compare figures 6a and 7).

Although the parameterization of the box model is apparently not fully adequate to describe the (non-linear) regimes of the coupled model, we have tried to estimate the coefficients of the box model parameterizations from the times series of the variables x and y as observed in the coupled model. Knowing both the variables and their time rates of change, we write, for instance, an estimate Z_i of as the linear combination at each time step i:

The unknown coefficients (a, b, c, d) are estimated by minimizing the mean square difference between the observed and the estimator Z_i. The coefficients of the box model that describe best the coupled model behavior can then be obtained. Because there is a significant model trend over the 6000 y of the experiment, the optimal fits were done on each 1000 y long time slices. Overall the parameterization captures most of the variations of . The estimated k and show some consistency between different time slices while g and y * are not very well constrained (even the sign of g changes). The correlation coefficients between and each term of the parameterizations support a tight fit with x only. The instability and the frictional processes appear as secondary influences. The mean values of the box model parameters found over the 6 independent time periods are: k = 0.19 y^-1 K^-1, = 3.65°C, g = 1.7´ 10^-5 Sv^-2 y^-1, y _* = 9.75 Sv with the last two showing much uncertainty.

The same procedure is applied to the temperature equation. It is only in the last 2000 years that the box model parameterizations captures most of the variation of , when the mean state does not evolve anymore. The most robust elements of the parameterization are the constant heat flux and the dependence on y x (which is better suited than a dependence in y alone). On the other hand the horizontal diffusion factor is not well defined whether in sign or amplitude.

Although it has been possible for box models to help in a physical understanding of the multiple steady states of the thermohaline circulation, this was not the situation for decadal to interdecadal oscillations and Ruddick and Zhang (1996) went as far as saying that "these had their roots in physical mechanisms not contained in the two box model". We propose here a solution to this problem that remains in the two boxes category but relies instead on a new physical mechanism. When the available potential energy in the ocean exceeds a given threshold, the overturning circulation becomes baroclinically unstable and increases exponentially. The increased heat transport then restores the available potential energy towards its original value. However the system does not converge to a steady state because of the existence of phase lags between the overturning and the available potential energy. The existence of such phase lags was proposed by Huck et al. (1998) to be caused by the finite propagation speed of planetary waves in the oscillatory states of OGCMs, and the instability mechanism has been attributed by CVH to the baroclinic instability of the oceanic circulation in regions of highest vertical shear that usually coincide with those of highest heat losses to the atmosphere. We have proposed to parameterize this mechanism by using Landau’s equation for the overturning and given the general conditions under which the system can oscillate. A Hopf type bifurcation to a limit cycle exists in the parameter space appropriate to the present state of the ocean-atmosphere system. On these time scales long compared to atmospheric adjustment time scales, the role of the atmosphere is one of passive adaptation to the ocean state. In agreement with GCMs behavior, it is demonstrated that a switch of the model to restoring boundary conditions to a frozen atmosphere drives the model solution back to steady state due to increased damping. Finally in nonlinear regimes, the oscillations of the temperature contrast show a marked asymmetry of evolution towards a saw tooth pattern (slow rise, more rapid decline) while the overturning remains at large amplitudes for a shorter fraction of the period. This behavior differs from that of the same variables observed in the coupled PGL/EBM model with a rapid rise of the temperature contrast followed by a slower decline. Given the results of the fit that was carried out between the coupled model variables and the box model parameterization, we may suspect that the reasons for the different behaviors may originate from different dissipation and diffusion processes operating in the coupled model since the fit was particularly poor for these processes.

Many of the OGCMs that have been run with flux boundary conditions exhibit decadal oscillations that do not depend on a two component (T,S) fluid and the present single component (T) box model parameterizes the baroclinic instability mechanism which these oscillations triggers. Because the role of the atmosphere is rather restricted on these long time scales, the choice of the parameters of the present climate system that we have used, suggest that there is no reason for the same mechanism to operate in coupled ocean — atmosphere circulation models. As in Landau’s early work on the genesis of the turbulence, the major difficulty is to derive the equation for the overturning from the hydrodynamical equations of motions. Past efforts in this direction include those of Marotzke et al. (1988), Wright and Stocker (1991), Wright et al. (1995) and Winton (1996). They derived equations for the overturning in the spirit of Stommel'’ 1961 formulation equilibrating buoyancy torque and friction. These two-dimensional studies in the latitude-depth plane failed to show decadal oscillations. This can now be understood with the help of figure 2. With overturning increasing with temperature (or buoyancy) anomalies, it is readily seen that if the temperature anomaly is larger than at steady state, the overturning is also larger and both effects contrive to increase the advection and damp the initial temperature anomaly. In contrast, quite recently Drbohlav and Jin (1998–DJ in what follows) have produced interdecadal oscillations using a 2D (latitude-depth) ocean model driven by constant flux. The result is puzzling in view of what was just said and also because we know that the essential ingredients, baroclinic instability and planetary waves, are absent in such a geometrical setting. What is then the nature of the oscillations and instability in their 2D model and to which extent is this a good analog of the 3D situation? An answer to this question can be provided by casting their formulation in terms of a two-layer model supposed for simplicity to have a thin upper thermocline layer h compared to the total depth. Only the baroclinic mode meridional velocity (the velocity difference between the upper and lower layer) is active because the barotropic mode is absent in such a rigid lid 2D model. According to DJ’s dynamics, the equations for the variables h and v can be cast as:

(14a)

(14b)

g’ is the reduced gravity and e a small coefficient used in DJ’s semi-empirical formulation, Q is the mass flux between the layers that parameterizes heating and cooling and F represents frictional effects. The novelty here is the presence of inertia in (14a) that introduces a phase lag between the density field and the overturning which permits oscillations. The small coefficient e is there to parameterize effects of the earth rotation.

Suppose that a mean state distribution of velocity and thickness (V,H) has been found to equilibrate a particular (but constant in time) heat flux distribution. The stability of that particular state can then be obtained from the linearized perturbation equations:

(15a)

(15b)

The variables h’ and v’ are the departures from the mean state and non-linear and frictional terms have been omitted in (15a) because their presence is not important for the present argument. Eliminating v’ between (15a) and (15b) yields:

(16)

The parameter c is simply (g’He )^1/2, the phase velocity of the waves that travel along the interface in the absence of a mean flow. The equation (16) is in fact telling us that the waves have the structure of internal gravity waves. Because they are slowed down enormously by the introduction of the e factor, they enter the range of interdecadal oscillations. Estimating g’ as expansion coefficient (2 10^-4°C^-1) times the thermal contrast between upper and slower layer (6°C), and H = 500 m, the true internal gravity wave speed (g’H)^1/2 is 2.5 m s^-1. Using e = 1.25 10^-5 the value used by DJ, the wave speed drops to 0.9 cm s^-1. Since typically structures of half a wavelength appear in their 6000 km domain, the estimated period of free waves for 12 000 km wavelength is 44 y, well into the range of interdecadal scales. Of course the presence of a mean flow modifies this. When the mean flow is constant, the modification reduces to a Döppler shift that alters the real wave speeds. More significantly, the last term in (16) shows that when the mean flow is convergent ( < 0), a linear instability arises whose growth rate is just controlled by the value of the convergence. (To see this, balance the first and last term in (16)). Consider regions of heat losses (Q < 0), where the mean heat (mass) transport (HV) is convergent. Suppose that the mean depth is perturbed to a slightly larger value (uniformly so that velocities are unchanged), then more heat is brought by the mean flow than can be extracted by the constant forcing and the layer continues to deepen. This is a simple mechanism that could perhaps account for the slow instability witnessed by DJ. Such an effect was mentioned in CVH but was judged weak when compared to baroclinic instability in interpreting three-dimensional simulations. It seems therefore that both the oscillations and the instabilities of this 2D model have a physical nature rather different than those observed in OGCMs and the model would therefore not qualify as a physical analog.

Maas (1994) also proposed low order model equations which were derived from an angular momentum principle. He kept the inertial terms and obtained a system with three degrees of freedom for the zonal, meridional and vertical density gradients. With this added freedom the system can now exhibit chaos but Maas pointed out to a state of 500 years period, self-sustained oscillations with the actual parameter values of the ocean. It will be interesting to compare his model with ours in the future, focussing specifically on decadal oscillations. In the mean time, we feel that it is appropriate to analyze the oscillations found in coupled ocean-atmosphere models to check if the instability mechanism exploited here that appears to summarize the linear regimes of simplified coupled ocean-atmosphere (EBM) simulations, may also be relevant in situations of much higher complexity.

Abstract *

1. Introduction *

2. The model *

3. Stability and oscillatory states *

4. Comparisons with a coupled ocean — atmosphere model *

5. Discussion *

References *

Figure Captions *