oral

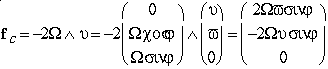
Cours ISEB 4. La Circulation Océanique

Océanographie - Environnement

________________________________________________________________________________

Pour la température: flux de chaleur sensible, flux de chaleur latente, rayonnement ondes courtes, rayonnement ondes longues.

Pour la quantité de mouvement: la tension de vent (composantes zonale et méridienne).

du/dt = ?u/?t + (u. grad) u = - 2 W x u - r₀^-1 grad p + friction (verticale et latérale)

On suppose l'océan découpé en fines couches d'épaisseur dz. On note T=(F, G) la tension turbulente horizontale s'exerçant dans l'océan (force d'entraînement communiquée d'une couche à l'autre).

La valeur de T à la surface est connue: il s'agit simplement de la tension exercée par le vent (t).

Le bilan des termes de friction verticale dans l'océan s'écrit, par une unité de masse: r₀^-1 ?T/?z.

La valeur de la tension turbulente au sein du fluide s'avère délicate à diagnostiquer, mais, par analogie avec les phénomènes de diffusion moléculaire, elle est le plus souvent choisie proportionnelle au gradient de la quantité diffusée: T = r₀ K ?u/?z, où K est un coefficient de viscosité turbulente (exprimé en m²/s) éventuellement variable dans le temps et l'espace (comme une fonction des propriétés de l'écoulement).

D'une manière analogue aux phénomènes de friction verticale, il est usuel d'exprimer la force de friction horizontale qui s'applique sur le fluide d'une manière équivalente aux phénomènes de diffusion moléculaire, avec un coefficient de viscosité (horizontale) le plus souvent constant. C'est donc un terme en laplacien qui vient s'ajouter aux équations du mouvement (ou, de façon plus élémentaire pour certaines études, un simple terme de rappel linéaire):

Dans la suite du chapitre, on s'intéressera souvent à des configurations stationnaires (indépendantes du temps), et on négligera aussi les termes d'accélération non linéaire et de friction horizontale.

avec F = r₀ K ?u/?z (avec F = t^x en surface), et G = r₀ K ?v/?z (et G = t^y en surface),

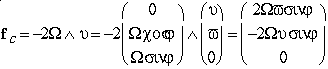
en désignant j la latitude, et f = 2 W sin j le paramètre de Coriolis, et en négligeant les vitesses verticales (w) devant les composantes de la vitesse horizontale (u, v).

Note: la masse volumique de l'océan est prise constante (r₀) dans ce système d'équations simplifiées, sauf dans l'équation hydrostatique (r); cette approximation est connue sous le nom d'approximation de Boussinesq et peut se justifier.

Ce sont elles qui initient le mouvement et déterminent les caractéristiques essentielles de la vitesse des couches océaniques.

La tension du vent communique de la quantité de mouvement à l'océan par entraînement frictionnel.

Les différences de densité (au sens de masse volumique) entre différents points de l'océan produisent des gradients de pression horizontaux propres à accélérer le fluide.

Elles influencent la direction et la nature de l'écoulement, mais ne sont pas explicitement motrices.

La force de Coriolis dévie les mouvements horizontaux de l'hémisphère nord sur leur droite.

La présence des continents agit comme une barrière, occasionnant un gradient horizontal de pression.

Une carte des courants moyens à la surface du globe (Fig. 1) fait apparaître 5 grands systèmes circulaires de courant qui sont des cellules de circulation (gyres) à l'échelle de bassins océaniques: Atlantique Nord, Atlantique Sud, Pacifique Nord, Pacifique Sud, Indien. Un sixième courant, le Courant Circumpolaire Antarctique, est encore plus intense (en terme de masse transportée) et s'écoule autour du continent Antarctique

Dans l'Atlantique et le Pacifique les gyres subtropicales convergent approximativement au niveau de l'ITCZ (zone de convergence intertropicale), avec apparition d'une dynamique spécifiquement équatoriale.

Les transports de masse associés aux gyres sont intenses: pour le Gulf Stream, le courant de bord ouest de l'Atlantique nord), la vitesse moyenne est de l'ordre de 8 km/h (2.2 m/s), la largeur moyenne de l'ordre de 70 km, et le débit moyen de l'ordre de 55 Sv (soit 55 Ž 10⁶ m³/s, alors que le début cumulé de tous les fleuves n'atteint que 1 Sv, et que le débit du plus grand, l'Amazone, seulement 0.2 Sv).

Le transport du Courant Circumpolaire Antarctique dépasse quant à lui les 100 Sv.

Les régions équatoriales sont caractérisées par des courants vers l'est situés légèrement au nord de l'équateur (contre courants équatoriaux), alors que les vents de surface soufflent vers l'ouest (les alizés) !

Le bassin Indien fait exception, car il est marqué par un très fort cycle saisonnier du fait de l'existence du régime de mousson.

Les paragraphes qui suivent vont donner des éléments permettant de comprendre les principaux équilibres associés à cette circulation de surface.

A l'état stationnaire, lorsque les effets non-linéaires et les effets visqueux sont négligeables, il y a équilibre sur l'horizontale entre la force de pression et la force de Coriolis (les deux premiers termes de l'équation précédente).

Cet équilibre, appelé équilibre géostrophique, se traduit par un mouvement du fluide sur la droite (gauche) de la force de gradient de pression dans l'hémisphère nord (sud), c'est à dire un mouvement le long des isobares (Fig. 2):

Cet équilibre est très largement vérifié à l'intérieur de l'océan, loin de l'équateur et des couches limites.

En dérivant l'équation précédente par rapport à z, et en utilisant l'équation hydrostatique, on déduit l'équation dite du "vent thermique", qui lie en chaque point le cisaillement vertical de vitesse au gradient horizontal de masse volumique:

La masse volumique est une quantité aisément mesurable dans l'océan (à partir de données de température, de salinité et de pression) alors que les mesures de vitesse sont beaucoup plus difficiles à réaliser. Les campagnes hydrologiques permettent d'établir des sections de masse volumique à partir desquelles on calcule la vitesse à chaque niveau, à partir d'une vitesse de référence à un niveau donné (par exemple mesurée directement avec un appareillage ADCP).

Pour l'atmosphère, la circulation (les vents) s'effectue en bonne approximation le long des isobares, en laissant sur la droite (dans l'hémisphère nord) les zones de haute pression (cf. régime de vent sur Brest) (Fig. 3).

En présence de friction, des deux termes impliqués dans l'équilibre géostrophique, seule la force de Coriolis est modifiée (moins intense car vitesse moindre). La circulation dans un anticyclone a donc une composante "sortante" (l'air expulsé est remplacé par de l'air descendant au sein de l'anticyclone), et la circulation dans une dépression une composante "entrante" (associé à des phénomènes d'ascendance).

Il est possible de dériver des relations intéressantes à partir de la simple relation hydrostatique.

On suppose que la surface de l'océan est à un niveau variable h, par rapport à une moyenne z = 0.

On peut intégrer l'équation hydrostatique entre un niveau z donné et la surface:

La force horizontale de pression (permettant le calcul de la vitesse géostrophique) s'écrit donc pour sa composante zonale:

Force(z) = - r₀^-1 ?P/?x = - r₀^-1 ?P_atm/?x - g r₀^-1 r(h) ?h/?x - g r₀^-1 _z?^? ?r/?x dz' (2)

où l'on a noté P(h) = P_atm la pression atmosphérique au niveau de la mer (note: une formulation identique s'applique pour la composante méridienne).

- l'effet direct du poids variable (dans l'espace) de l'atmosphère, et affectant l'océan de la même façon à chaque profondeur;

- un deuxième effet indépendant de la profondeur associé à la pente de la surface océanique;

- un effet associé à la structure interne en masse volumique de l'océan, et donc dépendant de la profondeur considérée.

En faisant l'hypothèse qu'il existe un niveau de référence, notons-le H, pour lequel la vitesse géostrophique est nulle, le gradient horizontal de pression (la seule force motrice considérée ici) doit s'annuler pour z = H, ce qui conduit à la relation:

On en déduit la force de pression à toute immersion, en fonction de ce niveau de référence H, par combinaison de (2) et (3):

Note : La vitesse géostrophique (ici méridienne) se déduit de cette force après division par le paramètre de Coriolis f (et utilisation du signe approprié):

Les effets de la pression atmosphériques sont équivalents à une correction du niveau de la mer de l'ordre de quelques centimètres sur des extensions horizontales de l'ordre de 100 km, et contribuent entre 1 à 10% au gradient horizontal de pression dans les couches de surface.

Toute la difficulté de ce calcul dit "calcul dynamique" provient de la détermination du niveau de référence, où la vitesse est considérée comme nulle. Pour caractériser les grands traits de la circulation océanique, on présente des cartes de hauteur dynamique (qui correspondent à l'intégration des anomalies de masse volumique par rapport à un niveau de référence donné).

Ces cartes permettent d'estimer le transport géostrophique entre deux niveaux choisis. Des gradients serrés de hauteur dynamique correspondent à de forts courants géostrophiques. On les trouve en particulier le long des bords ouest océaniques.

Écrivons les relations précédentes pour la vitesse géostrophique de surface (pour z = 0), avec le choix d'un niveau de référence H constant dans l'espace:

Le champ vectoriel f u apparaît donc horizontalement non divergent, il peut s'exprimer sous la forme d'une fonction de courant:

En pratique on utilise en fait une expression légèrement modifiée (faisant intervenir une constante additive):

L'intégrale définit alors une élévation, dont le tracé sur un plan horizontal renseigne sur les courants géostrophiques (Fig. 4).

Note: les dénivellations de hauteur dynamique sont de l'ordre du centième des dénivellations du niveau de la mer vues par un satellite et qui correspondent principalement à la surface du géoïde (modifiée par la bathymétrie).

L'expression la plus simple pour le terme de friction (correspondant à la propagation sur la verticale du signal d'entraînement lié au vent) est une valeur constante pour le paramètre de diffusion K.

(F, G)|_z=0 = (t^x, t^y) (la valeur de la tension à la surface est imposée par le vent)

Il se résout aisément sous forme complexe, et on obtient pour le profil vertical de u une spirale amortie avec la profondeur, appelée spirale d'Ekman.

de manière à satisfaire la seconde condition aux limites, il faut B = 0, et l'autre condition s'écrit:

On note que le module de la vitesse de surface prédite par la théorie d'Ekman vaut [r₀?(f K)]^-1 |t|, et que sa direction est à 45 degrés sur la droite du vent.

L'exacte spirale d'Ekman est souvent difficile à observer car l'océan de surface est agité par une forte turbulence qui tend à homogénéiser les mouvements dans les premières couches.

De plus les calculs sont ici faits avec une valeur constante du coefficient d'échange turbulent K, ce qui n'est pas forcément le cas pour l'océan réel.

Pour caractériser l'effet du vent dans les couches de surface, on préfère utiliser le concept du transport d'Ekman T_E (composantes U_E et V_E, exprimés en m²/s): on ne cherche pas à résoudre finement la structure verticale du mouvement mais à décrire le mouvement moyen, induit par le vent dans une couche dite "couche d'Ekman" et intégré de la surface jusqu'à la profondeur d'Ekman h_E, où l'on considère que les effets directs du vent deviennent négligeables (typiquement de l'ordre de quelques dizaines de mètres).

Pratiquement, la couche d'Ekman est souvent identifiée aux latitudes tempérées avec la couche de mélange où la température est uniforme.

On trouve après intégration verticale du système (4) et utilisation de la condition aux limites en surface:

Le transport d'Ekman se fait ainsi à 90° sur la droite du vent (pour l'hémisphère nord).

Dans l'Atlantique Nord, par exemple, la circulation des vents d'alizés dans les tropiques et des vents d'ouest aux latitudes tempérées, conduit à définir un transport d'Ekman convergent aux latitudes subtropicales.

Il est possible de diagnostiquer la vitesse verticale w_E qui apparaît à la base de la couche d'Ekman en intégrant l'équation de non divergence depuis h_E (la profondeur supposée constante de la couche d'Ekman) jusqu'à la surface, en notant que w = 0 à la surface:

Il ne faut pas oublier que le paramètre de Coriolis varie avec latitude (on ne peut le sortir du rotationnel), bien qu'en première approximation on puisse considérer que: w_E ? (r₀ f)^-1 rot_z t

Un anticyclone atmosphérique va donc occasionner une accumulation de masse en son centre à la surface de l'océan, et une vitesse d'échappement du fluide vers le bas. Cette accumulation de masse va modifier la répartition en densité dans l'océan de surface (en modifiant notamment la courbure de la surface), et peut engendrer une circulation secondaire géostrophique.

La circulation océanique est freinée par friction sur le fond marin. Cette friction correspond à un forçage de la circulation par des tensions turbulentes, analogues aux tensions de vent en surface. Il est donc possible d'introduire le concept de spirale d'Ekman de fond, équivalent à celui développé pour les couches de surface.

La présence d'un anticyclone atmosphérique (hautes pressions) induit une circulation anticyclonique dans l'océan.

En effet, en présence d'un anticyclone (atmosphérique), dans l'hémisphère nord, le transport d'Ekman dans la couche superficielle océanique est convergent (le vent chasse les eaux sur sa droite). Il y a alors création d'une zone de haute pression (élévation de l'interface air/mer, approfondissement de la base de la couche mélangée), propice au développement d'une circulation océanique de surface anticyclonique. Des phénomènes de downwelling apparaissent au milieu de cet anticyclone (l'eau "entassée" par le transport d'Ekman s'échappe vers le fond) (Fig. 6).

Une circulation inverse est obtenue en présence d'un cyclone (dépression) atmosphérique: le transport d'Ekman est divergent et crée une dépression propice au développement d'une circulation cyclonique, et à l'apparition de phénomènes d'upwelling (mouvements ascendants).

2. Interprétation de la circulation océanique de surface dans l'Atlantique Nord

Au cours des siècles sa description (ainsi que celle de l'ensemble de la circulation aux moyennes latitudes) a été affinée. Mais ce n'est que depuis la deuxième moitié du 20ème siècle que des théories consistantes en expliquent les principaux rouages.

Les gyres (cellules de circulation) subtropicales sont associées aux systèmes atmosphériques anticycloniques qui les surplombent (alizés dans les régions tropicales et vents d'ouest aux moyennes latitudes).

Cependant les centres des cellules atmosphériques ne coïncident pas avec les centres des cellules océaniques: les cellules atmosphériques sont plutôt centrées en milieu de bassin, tandis que les cellules océaniques ont leur centre plus à l'ouest, avec ainsi une intensification de la circulation sur les bords ouest.

Les courants de bord ouest observés (Kuroshio, Gulf Stream, ...) sont rapides, intenses (extension caractéristique: 100km, vitesse supérieure à 2m/s) et profonds. Les courants de bord est (Courant de Californie, Courant des Canaries) sont lents, larges et peu profonds.

On ne retient schématiquement que la structure zonale des vents, en négligeant de ce fait la composante nord/sud.

Les vents d'ouest sont schématiquement maxima vers 45°N, tandis que les alizés sont maxima vers 15°N. Vers 30°N, la composante zonale du vent est très faible.

Les vents exercent donc un couple sur l'océan, maximum à 30°N, et son intensité est donnée par le rotationnel du vent (sur lequel seule domine la variation méridienne de la composante zonale du vent).

Les vents ci-dessus ont tendance à accumuler les eaux vers 30°N (transport d'Ekman sur la droite du vent). Il s'y crée donc une région où de l'eau est continûment injectée vers les couches plus profondes de l'océan.

C'est Sverdrup qui le premier a décrit la circulation des gyres subtropicales, intégrée sur toute l'épaisseur de l'océan, en considérant la valeur de la vitesse verticale (pompage d'Ekman) à la base de la couche de surface.

En partant des équations (simplifiées) du mouvement valables pour l'océan loin des côtes (océan intérieur):

Et en prenant le rotationnel, on obtient une équation où la pression est absente:

En intégrant cette équation de la base de la couche active océanique, c'est à dire la profondeur au delà de laquelle il n'y a plus de mouvement, à la surface (deux immersions où la vitesse verticale s'annule), et en utilisant la relation de non divergence et le fait que la valeur de surface de la tension turbulente vaut t, il vient:

soit encore, en désignant par b le taux de variation du paramètre de Coriolis avec la latitude:

Cette relation est connue comme la relation de Sverdrup. Le transport total de masse méridien est déterminé à partir du rotationnel du vent uniquement (et est fonction de la latitude considérée par l'intermédiaire du paramètre b).

Connaissant la vitesse méridienne, il est possible d'obtenir la vitesse zonale, moyennée sur l'épaisseur de l'océan, en intégrant la relation de non divergence depuis le fond de la couche active vers la surface:

ce qui permet d'écrire, en supposant que le transport zonal est nul à la longitude x₀:

En prenant b constant, et en considérant que le champ de vent ne dépend pas de x, la relation devient simplement:

En choisissant t = (t^x, t^y) = (t₀ sin [(y - y₀)/?y] , 0) pour approximer le régime de vent autour de 30°N (y₀), on obtient: ? rot_zt / ?y = - ?²t^x / ?y² = {t₀ / (?y)²} sin [(y - y₀)/?y], c'est à dire un changement de signe autour de y₀.

Deux conventions sont possibles: choisir la côte est ou choisir la côte ouest pour la longitude à laquelle s'annule le transport zonal. Dans le cadre des travaux de Sverdrup, aucun argument ne permet en fait de motiver sérieusement l'un ou l'autre choix, et il est impossible de déduire le sens de la circulation qui s'installe dans le plan horizontal (Fig. 7).

Le transport méridien intégré sur toute l'étendue zonale d'un bassin comme l'Atlantique doit être nul (conservation de la masse), et il faut donc qu'au voisinage des côtes (là où les approximations faites ne sont plus valables) existe un courant de retour, violent, vers le nord.

Si l'on choisit un transport zonal nul à la côte est, on fait implicitement l'hypothèse que c'est à la côte ouest que se produit le courant de retour vers le nord, et la circulation est anticyclonique.

Dans le cas contraire, choix d'un transport zonal nul à la côte ouest, le courant de retour doit se faire à la côte est et la circulation dans le bassin doit être cyclonique (ce qui n'est pas vérifié par les observations).

Ce sont les travaux de Stommel, puis Munk, qui ont permis d'éclaircir cette ambiguïté en introduisant l'effet de termes jusqu'à présent négligés comme la friction horizontale (voir plus loin).

Il est possible de déterminer analytiquement la structure zonale de l'anticyclone ou du cyclone qui se crée dans l'océan en réponse au forçage de surface.

Il suffit pour cela d'intégrer les équations du mouvement sur toute la hauteur de l'océan actif.

On note h l'élévation de la surface. La pression à une immersion donnée est donnée par:

On note h_E la profondeur de la couche d'Ekman, choisie constante dans l'espace, et H la profondeur de la couche océanique active (plus bas l'océan est supposé au repos, et de densité r₀ + ?r). Les deux profondeurs sont algébriques (ici valeurs négatives). De manière à assurer l'absence de mouvement dans la dernière couche profonde, il faut que les gradients horizontaux de pression y soient nuls. Or la pression en dessous de l'immersion H est donnée par:

En utilisant les indices 1 et 2 pour dénoter les courants moyens dans la couche d'Ekman et dans la couche comprise entre les immersions h_E et H, et en intégrant les équations du mouvement sur ces couches respectives on obtient (en supposant h petit devant h_e):

w|_z=H = dH/dt = ?H/?t + u₂ ?H/?x + v₂ ?H/?y = 0 + g' f^-1 (?²H / ?y?x - ?²H / ?x?y) = 0

En remplaçant les vitesses par leur expression en fonction de H dans la relation de non-divergence, on obtient simplement:

Dans le cas d'une circulation atmosphérique anticyclonique, le second terme de l'équation est négatif. H étant choisi négatif, cela entraîne que H (algébrique) croît vers l'est, c'est à dire que l'océan actif est plus profond (et avec une surface plus élevée, du fait de la relation liant h à H) dans l'ouest que dans l'est du bassin.

Le premier terme est le pompage déjà diagnostiqué à la base de la couche d'Ekman. Le second terme est la correction apportée par les effets de pression (négligés dans le cadre de la théorie d'Ekman).

En plus de l'énergie et de la masse, la quantité de mouvement (linéaire et angulaire) est conservée (sous certaines conditions).

En océanographie, il est pratique de raisonner en termes de conservation de vorticité (plutôt que de conservation du moment angulaire, mais les deux quantités sont liées).

La vorticité d'un fluide est une quantité algébrique, et on la compte positive pour les échouements dans le sens inverse des aiguilles d'une montre (règle du tire-bouchon).

vorticité relative, x: il s'agit de la vorticité d'une particule en raison de son mouvement relatif par rapport à la Terre

vorticité planétaire, f: il s'agit de la vorticité d'une particule acquise du fait du mouvement de la Terre (en rotation par rapport à une référentiel absolu et fixe).

vorticité totale (ou absolue): c'est la somme de la vorticité relative et de la vorticité planétaire.

En l'absence de frottement et de forçage extérieur, la vorticité totale d'une particule se déplaçant sur l'horizontale est conservée.

Par exemple, une particule issue de l'équateur et se déplaçant vers le nord voit sa vorticité planétaire augmenter (f = 2 W sin j), et doit donc acquérir de la vorticité relative négative (anticyclonique).

On peut s'en convaincre en remarquant que la particule, en l'absence de friction, va être "distancée" par la Terre en rotation, et donc acquérir, par rapport à la Terre, de la vorticité relative.

Pour un fluide (et non plus une particule isolée) la situation est un peu plus complexe puisque la vorticité est à définir comme la somme des vorticités des particules individuelles. Pour une colonne fluide donnée, des phénomènes d'extension ou d'aplatissement vont occasionner une diminution ou une augmentation du diamètre de la colonne, et donc une augmentation ou une diminution de sa vorticité (exemple classique du patineur qui resserre ses bras, et s'allonge, pour tourner plus vite).

On introduit donc pour un fluide la notion de vorticité potentielle, (x + f)/|H|, où |H| est l'épaisseur de la colonne considérée (pour le patineur, f est négligeable devant x).

Dans l'océan ouvert, la valeur de f est généralement bien plus grande que la vorticité relative, et la conservation de la vorticité potentielle (? f/H) se traduit donc par des changements de latitude associés à des variations de l'épaisseur d'une colonne fluide.

Une illustration atmosphérique est par exemple la déflexion vers le sud du régime de vent d'ouest au passage du massif alpin.

On adapte les équations du mouvement pour un milieu à deux couches (une couche de surface active, de masse volumique r₀, d'épaisseur |H|, une couche de fond immobile de masse volumique r₀+?r), avec une formulation simplifiée pour la friction horizontale (un simple terme de rappel linéaire) et avec l'hypothèse d'une tension de vent distribuée sur toute l'épaisseur de la couche active:

En dérivant la première équation par rapport à y et la seconde par rapport à x on obtient une équation pour la vorticité relative (x = ?v/?x - ?u/?y) qui s'écrit:

?x/?t + u ?x/?x + v ?x/?y = - (f + x) (?u/?x + ?v/?y) - b v + r₀^-1 rot_z (t / H) - a x

soit encore, en utilisant le fait que df/dt = ?f/?t + u ?f/?x + v ?f/?y = 0 + 0 + b v,

H^-1 dx/?t + H^-1 df/dt - (f + x) H^-2 dH/dt = (r₀ H)^-1 rot_z (t / H) - a H^-1 x

Il y a donc bien conservation de la vorticité potentielle sur une trajectoire, en l'absence de forçage (t = 0) et de dissipation (a = 0).

Avec des arguments liés à la conservation de la vorticité, il est possible de montrer que le courant de retour violent vers le nord doit nécessairement apparaître sur le bord ouest des océans.

Des phénomènes de friction sont à prendre en compte, et c'est Stommel qui le premier a résolu le problème, en considérant le frottement du fluide au fond de l'océan. Munk a obtenu ensuite des résultats plus probants à partir de la friction latérale. Mais l'argumentation physique est identique.

On considère une particule qui effectue un trajet dans la cellule de circulation subtropicale, partant d'une latitude tropicale et se dirigeant vers le pôle (via un courant de bord), puis retournant à sa latitude initiale (transport vers le sud dans l'océan intérieur, cf. relation de Sverdrup).

On suppose atteint un régime stationnaire, et on suppose que l'épaisseur de la couche active est identique dans les parties nord et sud de l'écoulement. La vorticité relative de l'écoulement est également supposée petite en dehors des bords ouest et est du domaine où apparaissent sans doute des phénomènes frictionnels.

Une variation de vorticité potentielle entre les régions sud et nord du domaine est donc directement (et seulement) liée à une variation de la vorticité planétaire f. La vorticité totale augmente de la quantité ?f pour un mouvement vers le nord, et diminue de la même quantité pour un mouvement vers le sud.

- le couple exercé par le vent sur l'océan: source de vorticité négative (- |x_?|), virtuellement identique sur tout le bassin.

- la friction latérale à proximité des côtes: elle tend à s'opposer au mouvement du fluide, et elle est donc une source de vorticité positive (+ |x_fo|) quand le mouvement est anticyclonique, ou négative quand le mouvement est cyclonique (- |x_fe|). Son intensité est d'autant plus forte que la vorticité de l'écoulement est grande.

L'équation de conservation de vorticité totale permet alors d'écrire (à gauche pour un écoulement anticyclonique, et à droite pour un écoulement cyclonique):

On trouve donc une incompatibilité physique à l'existence d'une circulation cyclonique: |x_fe| ne saurait être négatif !

La seule circulation susceptible de s'installer est donc de type anticyclonique. La première relation de gauche permet de vérifier que la dissipation sera intense sur le bord ouest, dans la mesure où elle doit équilibrer un gain de vorticité planétaire et l'apport de vorticité par le vent. La seconde relation de gauche énonce simplement le fait que dans l'océan intérieur, l'apport de vorticité (négative) par le vent conduit à un mouvement vers l'équateur (baisse de la vorticité totale).

Le courant de retour, violent, de la gyre anticyclonique subtropicale est donc nécessairement dans la partie ouest des bassins (Fig. 8).

Note: de façon à retrouver les caractéristiques exactes des courants de bord ouest (intensité, échelle spatiale), il est nécessaire de prendre en compte précisément l'ensemble des termes de l'équation du mouvement, et notamment les termes non linéaires (advectifs).

Le mouvement méridien vers le sud des eaux de la couche profonde peut s'interpréter en termes de vorticité par la compression des colonnes de fluide occasionnée par l'injection d'eau continue vers le bas qui existe à la base de la couche d'Ekman.

La vorticité planétaire doit diminuer pour compenser l'écrasement de la colonne de fluide, on peut négliger x devant f dans (x + f)/H, et il y a donc mouvement vers l'équateur.

Le mouvement étant anticyclonique, c'est une région de haute pression qui se crée au centre de la gyre subtropicale (en fait plutôt décalée vers le bord ouest du bassin).

On peut repartir des équations de la section "circulation méridienne de Sverdrup", en incluant un terme de friction horizontale (rappel linéaire) dans les équations pour u et v. On écrit donc:

On intègre ensuite cette équation de la base de la couche active (où les termes de friction verticale et la vitesse verticale sont nulles) à la surface de l'océan (où la vitesse verticale est nulle, et où la friction verticale est donnée par la tension du vent):

Dans l'océan intérieur où la friction horizontale est négligeable on retrouve bien sûr la relation de Sverdrup habituelle.

Dans les régions où les phénomènes frictionnels vont dominer, il va y avoir un équilibre entre le courant de retour vers le nord, violent, et le terme de friction horizontale: dans ce cas V est positif, donc la vorticité relative de l'écoulement (intégrée sur la verticale) doit être négative, c'est à dire associée à une circulation localement anticyclonique. Ceci ne peut se produire que si le courant de retour se place sur le bord ouest.

Aux moyennes latitudes, le rotationnel du vent exercé sur l'océan (vents d'ouest à 45°N et alizés à 15°N) tend à accumuler les eaux au milieu du bassin subtropical.

Le transport d'Ekman convergent s'accompagne d'une injection continue de fluide dans les couches plus profondes de l'océan.

La théorie de Sverdrup indique que c'est vers le sud que se fait dans l'intérieur de l'océan (et loin des côtes) le mouvement méridien moyen.

Le courant de retour (nécessaire pour conserver la masse sur une section méridienne) s'effectue sur une couche limite sur le bord ouest (modèles de Stommel ou Munk).

Le premier point essentiel est ici l'annulation du paramètre de Coriolis à l'équateur: il n'y a pas de force de Coriolis.

Néanmoins, dès quelques degrés au nord ou au sud de l'équateur, la force devient suffisante pour affecter de façon notable les grands équilibres.

Ensuite, chaque océan est caractérisé par une zone de convergence intertropicale (là où les deux régimes d'alizés se rencontrent) située préférentiellement au nord de l'équateur (en moyenne annuelle), typiquement autour de 5 et 10°N.

Cette asymétrie (partiellement liée à l'inégalité de la répartition méridienne des continents) entraîne des répercussions importantes sur la structure des courants de surface.

Les régions de convergence à 30°N et S ont déjà été décrites (transport d'Ekman vers l'équateur associé aux vents d'ouest des latitudes moyennes, et transport vers les pôles associé aux alizés des basses latitudes).

La position plutôt nord de la zone de convergence intertropicale permet aux alizés du sud-est de traverser l'équateur. Au delà de 1°N et S, la dérive d'Ekman se fait sentir, et le transport d'Ekman est ainsi vers le pôle nord pour la composante des alizés du sud-est située au nord de l'équateur, et vers le pôle sud pour la composante des alizés du sud-est située au sud de l'équateur.

Du fait de l'affaissement des alizés au niveau de la zone de convergence équatoriale (zone des "calmes équatoriaux"), entre 5°N et 10°N, une région de convergence apparaît vers 5°N (accumulation d'eau par les alizés du sud-est), et une région de divergence apparaît vers 10°N (eaux chassées par les alizés du nord-est).

Chaque région de convergence est associée à une élévation de la surface de la mer, et à un affaissement de la thermocline. L'opposé se produit pour les régions de divergence.

En dehors de l'équateur même, où la force de Coriolis est virtuellement nulle, il est possible de définir le sens d'écoulement des courants géostrophiques sur l'axe ouest-est à partir de la pente de la surface, en écrivant que l'équilibre des forces se fait entre gradient méridien de pression et force de Coriolis.

Une élévation de la surface de l'océan (associée à un enfoncement de la thermocline) conduit à une zone de haute pression, laissée à sa droite par un courant géostrophique dans l'hémisphère nord (et à sa gauche dans l'hémisphère sud).

Entre 0° et 5°N: courant vers l'est, la composante nord du même Courant Équatorial Sud.

Alors qu'aux latitudes moyennes la rotation de la Terre entraîne l'apparition d'une spirale pour le courant directement induit par le vent, à l'équateur même les effets de friction correspondent à un signal de vitesse simplement transmis dans l'océan dans la direction du vent.

Le signal le plus fort est bien sûr en surface, puis décroît avec la profondeur pour devenir imperceptible à la base de la couche mélangée (au voisinage de la thermocline).

A ce signal de friction vient se superposer un signal de pression: les alizés chassant en continu les eaux équatoriales vers l'ouest du bassin, il s'y crée une accumulation d'eau (enfoncement de la thermocline et élévation de la surface) propre à l'apparition d'une force horizontale de pression dirigée d'ouest en est.

Cette force de pression est relativement homogène sur toute l'épaisseur de la couche de mélange (à la différence de la force de friction maximale en surface).

Ainsi dans les couches de surface les effets directs du vent dominent, et le courant est principalement accéléré vers l'ouest du bassin (Courant Équatorial Sud).

Plus en profondeur, mais toujours au dessus de la thermocline principale, les effets de pression dominent par contre les effets de friction, et le courant est principalement accéléré vers l'est (en sens contraire du vent de surface !): il s'agit du Sous-Courant Équatorial.

remarque: ce sont par exemple les phénomènes de diffusion (horizontale) ou les termes non linéaires qui permettent un équilibre des forces local.

Les alizés accumulant les eaux dans la parte ouest des bassins équatoriaux, la thermocline s'avère profonde dans l'ouest des bassins, et peu profonde dans l'est des bassins, et la surface a une structure opposée.

Cette simple dissymétrie zonale permet d'expliquer notamment l'existence du sous-courant, mais ne renseigne pas sur l'origine des gradients de température à la surface.

Ce sont les mouvements verticaux à l'équateur qui sont responsables du gradient zonal de température équatorial: la divergence équatoriale entraîne en effet un upwelling, perceptible sur tout le bassin, mais maximum au niveau du maximum de vent (centre du bassin).

Les vitesses verticales positives ramènent vers la surface des eaux froides (les eaux les plus chaudes sont au dessus des eaux froides, car c'est la température qui domine la salinité dans les effets sur la masse volumique).

Les eaux ramenées à la surface seront d'autant plus froides que la thermocline est proche de la surface. Ainsi, les eaux upwellées au milieu de bassin ont une température assez proche de la SST, et n'ont pas de signature sensible en surface). Au contraire les eaux upwellées dans la partie orientale des bassins tropicaux proviennent de la thermocline, et sont froides.

Ceci explique le développement des eaux les plus froides dans la partie orientale des bassins équatoriaux, en liaison également avec les processus d'upwelling côtier).

L'existence de ces eaux froides (23 à 24°C) dans les tropiques est fondamentale puisque c'est à ce niveau que se produisent les plus grands emmagasinages de chaleur par l'océan: la mer est chauffée par le soleil, mais il y a peu de perte par évaporation parce que les eaux sont relativement froides.

Dans l'hémisphère nord (HN), le vent (courant) géostrophique est parallèle aux isobares et laisse les hautes pressions sur sa droite. L'inverse se produit dans l'hémisphère sud (HS).

Vent d'ouest, tramontane, mistral. Une dépression sur l'Islande et une dépression sur le sud des Alpes, en association avec un anticyclone sur le sud-est de l'Espagne, peuvent expliquer ces vents par simple équilibre géostrophique, avec l'aide éventuelle de vallées d'intensification.

Topographie dynamique de la surface de la mer relative à l'immersion 1500 mètres. Le courant géostrophique de surface suit les isolignes de la fonction de courant, et est d'autant plus intense qu'elles sont rapprochées.

Spirale d'Ekman dans l'hémisphère nord. Le courant de surface est à 45° sur la droite du vent, et le transport intégré sur la couche d'Ekman est à 90° sur la droite du vent.

Forçage de l'océan profond par pompage d'Ekman. La vitesse d'Ekman est dirigée vers la surface dans le cas d'une circulation cyclonique, et vers le fond dans le cas d'une circulation anticyclonique.

Circulation de Sverdrup obtenue pour un transport zonal choisi nul à la paroi orientale. Une solution symétrique serait obtenue avec une condition analogue appliquée à la paroi occidentale. L'ambiguïté est levée en étudiant le comportement de la couche limite où se produit le courant de retour.

Circulation océanique forcée par le vent aux moyennes latitudes. La relation de Sverdrup donne le mouvement méridien dans le centre du bassin, tandis que le courant de retour vers le nord se fait dans une étroite couche limite de bord ouest.

Vision méridienne du régime des vents dans les tropiques, avec mention des régions de convergence et de divergence associée (transport d'Ekman).

Figure 10

Courants zonaux géostrophiques de surface, en réponse aux zones de convergence et de divergence présentes en région équatoriale.

Vision zonale, à l'équateur, des équilibres dynamiques entre terme de friction (entraînement des couches océaniques du fait du régime des vents de surface) et terme de pression (du fait de l'accumulation d'eau dans l'ouest du bassin). Les courants de surface (vers l'ouest) résultent d'un effet dominant du terme d'entraînement, alors qu'au niveau de la thermocline le Sous-Courant Équatorial coule en réponse au gradient zonal de pression.

20 septembre 11, 2003